
已知向量m=(2sinx,cosx),n=(cosx,2cosx),定义函数f(x)=m·n-1.
(1)求函数f(x)的最小正周期;
(2)确定函数f(x)的单调区间、对称轴与对称中心.
(1) ;(2)f(x)的单调递增区间是(kπ-
;(2)f(x)的单调递增区间是(kπ- ,kπ+),k∈Z;f(x)的单调递减区间是(kπ+,kπ+
,kπ+),k∈Z;f(x)的单调递减区间是(kπ+,kπ+ ),k∈Z;函数f(x)的对称轴为
),k∈Z;函数f(x)的对称轴为 ,k∈Z;函数f(x)的对称中心为
,k∈Z;函数f(x)的对称中心为 ,k∈Z .
,k∈Z .
【解析】
试题分析:(1)根据向量数量积的坐标运算得到函数 的解析式,化为标准式,然后利用周期公式
的解析式,化为标准式,然后利用周期公式 来求;(2) 根据正弦曲线的单调区间:
来求;(2) 根据正弦曲线的单调区间: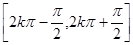 单调递增,
单调递增, 单调递减求目标函数的单调区间,对称轴是根据
单调递减求目标函数的单调区间,对称轴是根据 来求;对称中心是根据
来求;对称中心是根据 来求.
来求.
试题解析:(1)因为m·n=2sinxcosx+2cos2x 2分
=sin2x+cos2x+1, 4分
所以f(x)=2sin(2x+),
故T==π. 6分
(2)f(x)的单调递增区间是(kπ- ,kπ+),k∈Z, 8分
,kπ+),k∈Z, 8分
f(x)的单调递减区间是(kπ+,kπ+ ),k∈Z. 10分
),k∈Z. 10分
函数f(x)的对称轴为 ,k∈Z,
12分
,k∈Z,
12分
函数f(x)的对称中心为 ,k∈Z 14分
,k∈Z 14分
考点:平面向量、三角函数的图像与性质.


科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| 1 |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:山东省莱州一中2012届高三上学期模块检测数学理科试题 题型:044
已知向量m=(2sinx,2cosx),n=(![]() cosx,cosx),f(x)=m·n-1
cosx,cosx),f(x)=m·n-1
(1)求函数f(x)的最小正周期和单调递增区间;
(2)将函数y=f(x)的图象上各点的纵坐标保持不变,横坐标先缩短到原来的![]() ,把所得到的图象再向左平移
,把所得到的图象再向左平移![]() 单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
单位,得到函数y=g(x)的图象,求函数y=g(x)在区间![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源:辽宁省大连市、沈阳市2012届高三第二次联合考试数学文科试题 题型:044
已知向量m=(sin2+![]() ,sinx),n=(
,sinx),n=(![]() cos2x-
cos2x-![]() sin2x,2sinx),函数f(x)=m·n.
sin2x,2sinx),函数f(x)=m·n.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若![]() ,求函数f(x)值域.
,求函数f(x)值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知向量m=(2sinx,cosx),n=(![]() cosx,2cosx),定义函数f(x)=m·n-1.
cosx,2cosx),定义函数f(x)=m·n-1.
(1)求函数f(x)的最小正周期;
(2)确定函数f(x)的单调区间、对称轴与对称中心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com