
分析 根据题意,结合对数函数的图象与性质,利用复合函数的性质,求出函数y的最大与最小值,
再列出方程组,求出a、b的值.
解答 解:∵0<a<1,x∈[2,4];
∴logax∈[loga4,loga2],
∴y=${{(log}_{a}x)}^{2}$-2logax+b的最大值是
ymax=${{(log}_{a}4)}^{2}$-2loga4+b=8,
最小值是ymin=${{(log}_{a}2)}^{2}$-2loga2+b=$\frac{25}{4}$;
∴ymax-ymin=${{(log}_{a}4)}^{2}$-2loga4-${{(log}_{a}2)}^{2}$+2loga2=$\frac{7}{4}$,
化简得12${{(log}_{a}2)}^{2}$-8loga2-7=0,
解得loga2=-$\frac{1}{2}$或loga2=$\frac{7}{6}$,
即a=$\frac{1}{4}$或a=${2}^{\frac{6}{7}}$(大于1,应舍去);
当a=$\frac{1}{4}$时,b=5.
综上,a=$\frac{1}{4}$、b=5.
点评 本题考查了对数函数的图象与性质的应用问题,也考查了复合函数的单调性问题,考查了方程组的应用问题,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD中,AB∥DC,AB,BC,DC,AD(或其延长线)分别与平面M相交于E,F,G,H,求证:E,F,G,H必在同一直线上.
如图,四边形ABCD中,AB∥DC,AB,BC,DC,AD(或其延长线)分别与平面M相交于E,F,G,H,求证:E,F,G,H必在同一直线上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
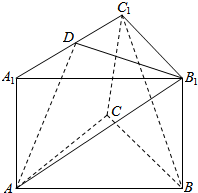 如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.
如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com