
知{an}是首项为-2的等比数列,Sn是其前n项和,且S3,S2,S4成等差数列,
(1)求数列{an}的通项公式.
(2)若bn=log2|an|,求数列{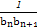 }的前n项和Tn.
}的前n项和Tn.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
已知等差数列{an}的前n项和为Sn,n∈N*,且满足a2+a4=14,S7=70.
(1)求数列{an}的通项公式;
(2)若bn=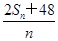 ,则数列{bn}的最小项是第几项,并求该项的值.
,则数列{bn}的最小项是第几项,并求该项的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(1)已知两个等比数列{an},{bn},满足a1=a(a>0),b1-a1=1,b2-a2=2,b3-a3=3,若数列{an}唯一,求a的值;
(2)是否存在两个等比数列{an},{bn},使得b1-a1,b2-a2,b3-a3,b4-a4成公差不为0的等差数列?若存在,求{an},{bn}的通项公式;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
等差数列{an}的首项为a1,公差d=-1,前n项和为Sn.
(1)若S5=-5,求a1的值.
(2)若Sn≤an对任意正整数n均成立,求a1的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=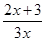 (x>0),数列{an}满足a1=1,an=f
(x>0),数列{an}满足a1=1,an=f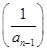 (n∈N*,且n≥2).
(n∈N*,且n≥2).
(1)求数列{an}的通项公式;
(2)设Tn=a1a2-a2a3+a3a4-a4a5+…+(-1)n-1·anan+1,若Tn≥tn2对n∈N*恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设正项数列{an}的前n项和是Sn,若{an}和{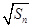 }都是等差数列,且公差相等.
}都是等差数列,且公差相等.
(1)求{an}的通项公式;
(2)若a1,a2,a5恰为等比数列{bn}的前三项,记数列cn=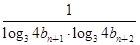 ,数列{cn}的前n项和为Tn,求Tn.
,数列{cn}的前n项和为Tn,求Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com