
分析 (1)利用辅助角公式和二倍角基本公式将函数化为y=Asin(ωx+φ)的形式,结合三角函数的图象和性质,即可求实数a以及f(x)的取值最小值.
解答 解:函数$f(x)=asinxcosx-{sin^2}x+\frac{1}{2}$=$\frac{a}{2}$sin2x-$\frac{1}{2}$+$\frac{1}{2}$cos2x+$\frac{1}{2}$=$\sqrt{\frac{{a}^{2}+1}{4}}$sin(2x+θ),tanθ=$\frac{1}{a}$.
函数的对称轴方程为2x+θ=$\frac{π}{2}$+kπ,(k∈Z)
对称轴方程为$x=\frac{π}{6}$,即$\frac{π}{3}+θ$=$\frac{π}{2}$+kπ,
可得θ=$\frac{π}{6}$+kπ,
∵tanθ=$\frac{1}{a}$.
∴$\frac{1}{a}$=tan($\frac{π}{6}+kπ$)=tan$\frac{π}{6}$=$\frac{\sqrt{3}}{3}$,
故a=$\sqrt{3}$
当2x+θ=$\frac{π}{2}+2kπ$时,函数f(x)取得最大值为1.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,属于基础题


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | $\sqrt{15}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
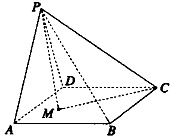 如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹的长度为$\sqrt{5}$.
如图,在四棱锥P-ABCD中,侧面PAD为正三角形,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的轨迹的长度为$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 表示一个算法的起始和结束,程序框是 | |
| B. | 表示一个算法输入和输出的信息,程序框是 | |
| C. | 表示一个算法的起始和结束,程序框是 | |
| D. | 表示一个算法输入和输出的信息,程序框是 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com