
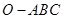 的侧棱
的侧棱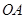 、
、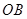 、
、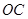 两两垂直,且
两两垂直,且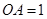 ,
,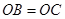
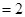 ,
,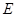 是
是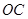 的中点.
的中点.
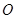 点到面
点到面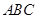 的距离;
的距离;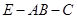 的正弦值.
的正弦值. ;(2)
;(2) .
.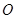 到平面
到平面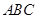 的距离,具体做法是:先利用
的距离,具体做法是:先利用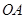 、
、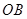 、
、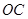 两两垂直以及它们的长度计算出三棱锥
两两垂直以及它们的长度计算出三棱锥 的体积,然后将此三棱锥转换成以点
的体积,然后将此三棱锥转换成以点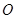 为顶点,以
为顶点,以 所在平面为底面的三棱锥通过体积来计算点
所在平面为底面的三棱锥通过体积来计算点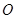 到平面
到平面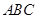 的距离;解法二是直接利用空间向量法求点
的距离;解法二是直接利用空间向量法求点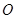 到平面
到平面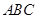 的距离;(2)解法一是通过三垂线法求二面角
的距离;(2)解法一是通过三垂线法求二面角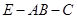 的正弦值,即
的正弦值,即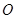 在平面
在平面 内作
内作 ,垂足为点
,垂足为点 ,连接
,连接 、
、 ,证明
,证明 ,
, ,从而得到
,从而得到 为二面角
为二面角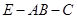 的平面角,再选择合适的三角形求出
的平面角,再选择合适的三角形求出 的正弦值;解法二是直接利用空间向量法求二面角
的正弦值;解法二是直接利用空间向量法求二面角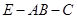 的余弦值,进而求出它的正弦值.
的余弦值,进而求出它的正弦值. 的中点
的中点 ,连接
,连接 、
、 ,
,
 ,
, ,且
,且 ,
, 平面
平面 ,
, 平面
平面 ,
, 平面
平面 ,
, 平面
平面 ,
, ,
,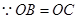 ,
, 为
为 的中点,
的中点, ,
,  ,
, 平面
平面 ,
, 平面
平面 ,
, 平面
平面 ,
, 平面
平面 ,
, ,
, ,且
,且 ,
, ,
, 为
为 的中点,
的中点, ,
, 平面
平面 ,
, 平面
平面 ,
, ,
, ,
, ,
, ,
, ,
,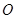 到平面
到平面 的距离为
的距离为 ,由等体积法知,
,由等体积法知, ,
, ,即
,即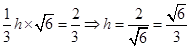 ,即点
,即点 到平面
到平面 的距离为
的距离为 ;
;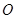 在平面
在平面 内作
内作 ,垂足为点
,垂足为点 ,连接
,连接 ,
,
 ,
, ,
, ,
, 平面
平面 ,
, 平面
平面 ,
, 平面
平面 ,即
,即 平面
平面 ,
, 平面
平面 ,
, ,又
,又 ,
, ,
, 平面
平面 ,
, 平面
平面 ,
, 平面
平面 ,
, 平面
平面 ,
, ,
,  ,
, ,
, ,
, ,
, ,
, ,故二面角
,故二面角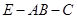 的平面角为
的平面角为 ,
, ,
, 中,
中, ,
, 中,
中, ,
, ,
, ,
, ,
, ,
,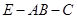 的正弦值为
的正弦值为 ;
;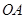 、
、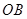 、
、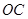 两两垂直,不妨以点
两两垂直,不妨以点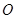 为坐标原点,
为坐标原点,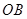 、
、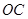 、
、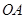 所在直线分别为
所在直线分别为 轴、
轴、 轴、
轴、 轴建立如下图所示的空间直角坐标系,
轴建立如下图所示的空间直角坐标系,
 ,
, ,
, ,
, ,
,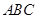 的一个法向量为
的一个法向量为 ,
, ,
, ,
, ,
, ,
, ,可得平面
,可得平面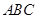 的一个法向量为
的一个法向量为 ,而
,而 ,
, ,
, ,
,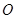 到平面
到平面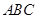 的距离为
的距离为 ,则
,则 ,
,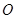 到平面
到平面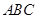 的距离为
的距离为 ;
; 的一个法向量为
的一个法向量为 ,
, ,
, ,
, ,
, ,
, ,可得平面
,可得平面 的一个法向量为
的一个法向量为 ,
, ,
, ,
, ,
,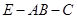 的平面角为
的平面角为 ,则
,则 为锐角,
为锐角, ,
, ,
,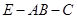 的正弦值为
的正弦值为 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题

 的正切值.
的正切值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,
, 与平面
与平面 ,
, 交于
交于 两点。给出以下命题,其中真命题有________(写出所有正确命题的序号)
两点。给出以下命题,其中真命题有________(写出所有正确命题的序号)
 为线段
为线段 的两个三等分点;
的两个三等分点; ;
; 中点为
中点为 ,
, 的中点为
的中点为 ,则直线
,则直线 与面
与面 有一个交点;
有一个交点; 为
为 的内心;
的内心; 为
为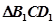 的外心,则
的外心,则 为定值.
为定值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com