
| �ɼ� | ���� |
| A | 9 |
| B | 12 |
| C | 31 |
| D | 22 |
| E | 6 |
���� ��1��������80���У���12��ѧ���ɼ��ȼ�ΪB�����Կ��Թ��Ƹ�Уѧ����óɼ��ȼ�ΪB�ĸ���Ϊ$\frac{12}{80}$�����ɵó���У�߶��꼶ѧ����óɼ�ΪB��������
��2��������80��ѧ���ɼ���ƽ����Ϊ��$\frac{1}{80}$��9��100+12��80+31��60+22��40+6��20����
��3���ɼ�ΪA��B��ͬѧ�ֱ���9�ˣ�12�ˣ������ֲ������ȡ7���гɼ�ΪA����3�ˣ��ɼ�ΪB����4�ˣ�������ɵã�P��X=k��=$\frac{{∁}_{3}^{k}{∁}_{4}^{3-k}}{{∁}_{7}^{3}}$��k=0��1��2��3��
��� �⣺��1��������80���У���12��ѧ���ɼ��ȼ�ΪB��
���Կ��Թ��Ƹ�Уѧ����óɼ��ȼ�ΪB�ĸ���Ϊ$\frac{12}{80}=\frac{3}{20}$������2�֣�
���У�߶��꼶ѧ����óɼ�ΪB������Լ��1000��$\frac{3}{20}$=150������3�֣�
��2��������80��ѧ���ɼ���ƽ����Ϊ��
$\frac{1}{80}$��9��100+12��80+31��60+22��40+6��20��=59������4�֣�
��59��60����˸�У�߶��꼶�˽ν�ѧδ��ꡭ��6�֣�
��3���ɼ�ΪA��B��ͬѧ�ֱ���9�ˣ�12�ˣ�
�����ֲ������ȡ7���гɼ�ΪA����3�ˣ��ɼ�ΪB����4�ˡ���7�֣�
��������ɵã�P��X=k��=$\frac{{∁}_{3}^{k}{∁}_{4}^{3-k}}{{∁}_{7}^{3}}$��k=0��1��2��3��
��P��X=0��=$\frac{4}{35}$��P��X=1��=$\frac{18}{35}$��P��X=2��=$\frac{12}{35}$��P��X=3��=$\frac{1}{35}$.10�֣�
����EX=0+1��$\frac{18}{35}$+2��$\frac{12}{35}$+3��$\frac{1}{35}$=$\frac{9}{7}$.10�֣�
���� ���⿼����ƽ�������ֲ�����������ηֲ��и��ʼ��㹫ʽ������ѧ������������������������������������е��⣮


 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ڡ�ABC�У���A=��B��sin��A=sin��B�ij�Ҫ���� | |
| B�� | ���⡰��|x|��|y|����x��y���ķ������ǡ���|x|��|y|����x��y�� | |
| C�� | ������a+bi����1+i���븴��-1+3i��ȵij�Ҫ�����ǡ�a=1��b=2�� | |
| D�� | ���⡰?x�ʣ�0��+�ޣ���2x��1���ķ��ǡ�?x0�ʣ�-�ޣ�0]��2${\;}^{{x}_{0}}$��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{128}$ | B�� | $\frac{1}{256}$ | C�� | $\frac{1}{512}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 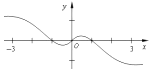 | B�� | 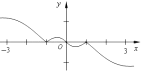 | ||
| C�� | 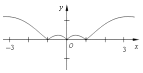 | D�� | 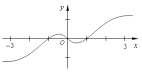 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=0.4x+2.3 | B�� | y=2x+2.4 | C�� | y=-2x+9.5 | D�� | y=-0.4x+4.4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com