Question

【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关，现对100名五年级学生进行了问卷调查，得到如下2×2列联表，平均每天喝500ml以上为常喝，体重超过50kg为肥胖．

	不常喝	常喝	合计
肥胖	x	y	50
不肥胖	40	10	50
合计	A	B	100

现从这100名儿童中随机抽取1人，抽到不常喝碳酸饮料的学生的概率为
（1）求2×2列联表中的数据x，y，A，B的值；
（2）根据列联表中的数据绘制肥胖率的条形统计图，并判断常喝碳酸饮料是否影响肥胖？
（3）是否有99.9%的把握认为肥胖与常喝碳酸饮料有关？说明你的理由． 附：参考公式：K2= ，其中n=a+b+c+d．
临界值表：

P（K2≥k）	0.05	0.025	0.010	0.005	0.001
k	3.841	5.024	6.635	7.879	10.828

Answer 1

【答案】
（1）解：根据题意，不常喝碳酸饮料的学生为A=100× =60，∴x=60﹣40=20，y=50﹣20=30，B=30+10=40
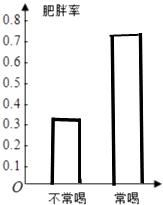
（2）解：根据列联表中的数据得常喝饮料的肥胖率为 =0.75，

不常喝饮料的肥胖率为 =0.33，

绘制肥胖率的条形统计图如图所示；

根据统计图判断常喝碳酸饮料会增加肥胖的可能

（3）解：由已知数据可求得：K2= ≈15.629＞7.879，

因此有99.5%的把握认为肥胖与常喝碳酸饮料有关．

【解析】（1）根据题意，计算不常喝碳酸饮料的学生A，以及对应表中x、y和B的值；（2）根据列联表中的数据计算常喝饮料与不常喝饮料的肥胖率，绘图即可；根据统计图即可得出概率结论；（3）计算观测值K2 ， 对照数表即可得出结论．