

思路解析:观察图形,易猜测CE∥DF,再由四点共圆及圆周角可证明猜测,注意作图时的各种情形.
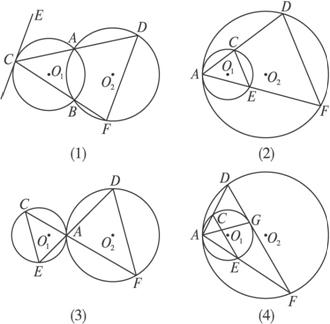
解:作出各种情形的图如下,观察图形,易猜测CE∥DF.

在图(1)中,连结AB,由圆内接四边形ABEC,可得∠ACE=∠ABF;又由圆内接四边形ABFD,可得∠ABF+∠ADF=180°.所以,∠ACE+∠ADF=180°,得到CE∥DF.
在图(2)中,连结AB,由圆周角,可得∠ACE=∠ABE;又由圆内接四边形ABFD,可得∠ABE=∠ADF.所以,∠ACE=∠ADF,得到CE∥DF.
在图(3)中,连结AB,由⊙O1圆周角,可得∠ACE=∠ABE;又由⊙O2圆周角,可得∠ABE=∠ADF.所以,∠ACE=∠ADF,得到CE∥DF.
所以,各种情形都有CE∥DF.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
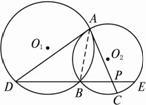
图2-5-18
(1)求证:AD∥EC;
(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
求证:![]() .
.
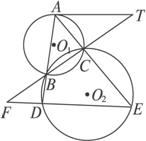
图2-25
查看答案和解析>>
科目:高中数学 来源: 题型:
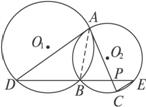
图2-5-11
(1)求证:AD∥EC;
(2)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com