
| 消费指数(百元) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) |
| 人数 | 3 | 4 | 6 | 5 | 2 |
| 消费指数(百元) | [3,4) | [4,5) | [5,6) | [6,7) | [7,8] |
| 人数 | 9 | 36 | a | 54 | 9 |
分析 (1)求出A、B两组应抽取的人数是多少,再求a的值;计算A、B组中各小组对应的频率,画出对应的频率分布直方图;
(2)计算A、B组游客的平均消费指数,再求出这1000名游客消费的平均数.
解答 解:(1)∵A组抽取的人数是3+4+6+5+2=20,
∴B组应抽取的人数是9+36+a+54+9=20×9,
解得a=72;
计算A组中各小组对应的频率是
[1,2)0.15,[2,3)0.2,[3,4)0.3,[4,5)0.25,[5,6)0.1;
B组中各小组对应的频率是
[3,4)0.05,[4,5)0.2,[5,6)0.4,[6,7)0.3,[7,8]0.05;
画出A组与B组的频率分布直方图,如图所示: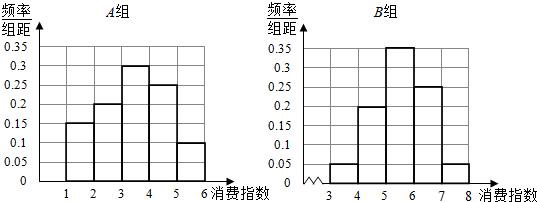
(2)A组游客的平均消费指数为:
$\frac{3}{2}×\frac{3}{20}+\frac{5}{2}×\frac{4}{20}+\frac{7}{2}×\frac{6}{20}+\frac{9}{2}×\frac{5}{20}+\frac{11}{2}×\frac{2}{20}=3.45$,
B组游客的平均消费指数为:
$\frac{7}{2}×\frac{9}{180}+\frac{9}{2}×\frac{36}{180}+\frac{11}{2}×\frac{72}{180}+\frac{13}{2}×\frac{54}{180}+\frac{15}{2}×\frac{9}{180}=5.6$;
则这1000名游客消费的平均数为
3.45×0.1+5.6×0.9=5.285.
点评 本题考查了频率分布直方图的应用问题,也考查了分层抽样方法与平均数的应用问题,是基础题目.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a⊥c,b⊥c,则a∥b | B. | 若α⊥γ,β⊥γ,则α∥β | C. | 若α⊥a,β⊥a,则α∥β | D. | 若a⊥α,b⊥a,则b∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 12π | C. | 16π | D. | 64π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 8π | C. | 4π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3c+3a=2 | B. | 3c+3a>2 | ||
| C. | 3c+3a<2 | D. | 3c+3a与2的大小关系不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com