
【题目】已知抛物线y2=﹣x与直线y=k(x+1)相交于A(x1 , y1),B(x2 , y2)两点,O为坐标原点.
(1)求y1y2的值;
(2)求证:OA⊥OB.
 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】已知直线l1:x﹣2y+3=0和l2:x+2y﹣9=0的交点为A.
(1)求过点A,且与直线2x+3y﹣1=0平行的直线方程;
(2)求过点A,且倾斜角为直线l1倾斜角2倍的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米.最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ. 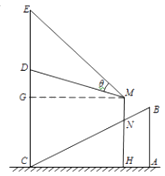
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米,视角θ最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(a﹣2)x﹣2,a∈R.
(1)若关于x的不等式f(x)≤0的解集为[﹣1,2],求实数a的值;
(2)当a<0时,解关于x的不等式f(x)≤0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,角A,B,C的对边分别是a,b,c,且bsinA+acosB=0.
(1)求角B的大小;
(2)若b=2,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的最下正周期为π,且点P(
)的最下正周期为π,且点P( ![]() ,2)是该函数图象的一个人最高点.
,2)是该函数图象的一个人最高点.
(1)求函数f(x)的解析式;
(2)若x∈[﹣ ![]() ,0],求函数y=f(x)的值域;
,0],求函数y=f(x)的值域;
(3)把函数y=f(x)的图线向右平移θ(0<θ< ![]() )个单位,得到函数y=g(x)在[0,
)个单位,得到函数y=g(x)在[0, ![]() ]上是单调增函数,求θ的取值范围.
]上是单调增函数,求θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知向量 ![]() ,
, ![]() ,定点
,定点 ![]() 的坐标为
的坐标为 ![]() ,点
,点 ![]() 满足
满足 ![]() ,曲线
,曲线 ![]() ,区域
,区域 ![]() ,曲线
,曲线 ![]() 与区域
与区域 ![]() 的交集为两段分离的曲线,则( )
的交集为两段分离的曲线,则( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,满足2asinA=(2b﹣ ![]() c)sinB+(2c﹣
c)sinB+(2c﹣ ![]() b)sinC. (Ⅰ)求角A的大小;
b)sinC. (Ⅰ)求角A的大小;
(Ⅱ)若a=2,b=2 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com