
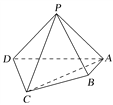
【题目】(2016·北京卷)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=![]() .
.
(1)求证:PD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值;
(3)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1) 见解析,(2)![]() ,(3)
,(3)![]()
【解析】试题分析:(1)先根据面面垂直性质定理得AB⊥平面PAD,即得AB⊥PD,再根据PA⊥PD,由线面垂直判定定理得结论, (2) 先根据条件建立空间直角坐标系,设立各点坐标,根据方程组解平面PCD法向量,根据向量数量积求向量夹角,最后根据线面角与向量夹角互余关系求直线PB与平面PCD所成角的正弦值;(3)由 BM∥平面PCD得向量BM与平面法向量垂直,根据向量数量积为零,解得![]() 的值.
的值.
试题解析: (1)证明 ∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,又AB⊥AD,AB平面ABCD,
∴AB⊥平面PAD.∵PD平面PAD.∴AB⊥PD.
又PA⊥PD,PA∩AB=A,
∴PD⊥平面PAB.

(2)解 取AD中点O,连接CO,PO,∵PA=PD,∴PO⊥AD.
又∵PO平面PAD,平面PAD⊥平面ABCD,
∴PO⊥平面ABCD.
∵CO平面ABCD,∴PO⊥CO.
∵AC=CD,∴CO⊥AD.
以O为原点建立如图所示空间直角坐标系.易知P(0,0,1),B(1,1,0),D(0,-1,0),C(2,0,0).
则![]() =(1,1,-1),
=(1,1,-1),![]() =(0,-1,-1),
=(0,-1,-1),![]() =(2,0,-1).
=(2,0,-1).
![]() =(-2,-1,0).
=(-2,-1,0).
设n=(x0,y0,1)为平面PDC的一个法向量.
由 得
得![]() 解得
解得
即n=![]() .
.
设PB与平面PCD的夹角为θ.
则sin θ=|cos〈n,![]() 〉|=
〉|= =
=
=![]() .
.
(3)解 设M是棱PA上一点,则存在λ∈[0,1]使得![]() =λ
=λ![]() ,因此点M(0,1-λ,λ),
,因此点M(0,1-λ,λ),![]() =(-1,-λ,λ).因为BM平面PCD,所以BM∥平面PCD,
=(-1,-λ,λ).因为BM平面PCD,所以BM∥平面PCD,
当且仅当![]() ·n=0,即(-1,-λ,λ)·
·n=0,即(-1,-λ,λ)·![]() =0,解得λ=
=0,解得λ=![]() ,所以在棱PA上存在点M使得BM∥平面PCD,此时
,所以在棱PA上存在点M使得BM∥平面PCD,此时![]() =
=![]() .
.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() 和圆
和圆![]() :
:![]() ,给出下列说法:①直线
,给出下列说法:①直线![]() 和圆
和圆![]() 不可能相切;②当
不可能相切;②当![]() 时,直线
时,直线![]() 平分圆
平分圆![]() 的面积;③若直线
的面积;③若直线![]() 截圆
截圆![]() 所得的弦长最短,则
所得的弦长最短,则![]() ;④对于任意的实数
;④对于任意的实数![]() ,有且只有两个
,有且只有两个![]() 的取值,使直线
的取值,使直线![]() 截圆
截圆![]() 所得的弦长为
所得的弦长为![]() .其中正确的说法个数是( )
.其中正确的说法个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,AB=PA=2,PA⊥平面ABCD,E是PC的中点,F是AB的中点.

(1)求证:BE∥平面PDF;
(2)求证:平面PDF⊥平面PAB;
(3)求BE与平面PAC所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为![]() ,墙
,墙![]() 的长度为
的长度为![]() 米,(已有两面墙的可利用长度足够大),记
米,(已有两面墙的可利用长度足够大),记![]() .
.
(1)若![]() ,求
,求![]() 的周长(结果精确到0.01米);
的周长(结果精确到0.01米);
(2)为了使小动物能健康成长,要求所建的三角形露天活动室面积,![]() 的面积尽可能大,当
的面积尽可能大,当![]() 为何值时,该活动室面积最大?并求出最大面积.
为何值时,该活动室面积最大?并求出最大面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:

(1)求分数![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】寒冷的冬天,某高中一组学生来到一大棚蔬菜基地,研究种子发芽与温度控制技术的关系,他们分别记录五组平均温度及种子的发芽数,得到如下数据:
平均温度 | 11 | 10 | 13 | 9 | 12 |
发芽数 | 25 | 23 | 30 | 16 | 26 |
(Ⅰ)若从五组数据中选取两组数据,求这两组数据平均温度相差不超过![]() 概率;
概率;
(Ⅱ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)若由线性回归方程得到的估计数据与实际数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(Ⅱ)屮所得的线性回归方程是否可靠?
(注:  ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,对称轴为坐标轴,椭圆
的中心在原点,对称轴为坐标轴,椭圆![]() 与直线
与直线![]() 相切于点
相切于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点(
两点(![]() ,
, ![]() 不是长轴端点),且以
不是长轴端点),且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 在
在![]() 轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.
轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角![]() 和以
和以![]() 为直径的半圆拼接而成,点
为直径的半圆拼接而成,点![]() 为半圈上一点(异于
为半圈上一点(异于![]() ,
,![]() ),点
),点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,
,![]() ,设
,设![]() .
.

(1)为了使工艺礼品达到最佳观赏效果,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,工艺礼品达到最佳观赏效果;
为何值时,工艺礼品达到最佳观赏效果;
(2)为了工艺礼品达到最佳稳定性便于收藏,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,
为何值时,![]() 取得最大值,并求该最大值.
取得最大值,并求该最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com