
【题目】已知函数f(x)= ![]() 是定义在R上的奇函数,且f(1)=2.
是定义在R上的奇函数,且f(1)=2.
(1)求实数a,b并写出函数f(x)的解析式;
(2)判断函数f(x)在(﹣1,1)上的单调性并加以证明.
【答案】
(1)解:∵函数f(x)= ![]() 是定义在R上的奇函数,
是定义在R上的奇函数,
∴f(0)=0,
又由f(1)=2.
故 ![]() ,
,
解得:a=4,b=0,
f(x)= ![]()
(2)解:函数f(x)在(﹣1,1)上的单调递增,理由如下:
∵f(x)= ![]() ,
,
∴f′(x)= ![]() ,
,
当x∈(﹣1,1)时,f′(x)≥0恒成立,
故函数f(x)在(﹣1,1)上的单调递增
【解析】(1)根据奇函数的特性,可得f(0)=0,又由f(1)=2.可得实数a,b的值,进而得到函数f(x)的解析式;(2)求导,分析导数的符号,进而判断函数f(x)在(﹣1,1)上的单调递增.
【考点精析】根据题目的已知条件,利用函数单调性的判断方法和利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(0,+∞),f(2)=1,f(xy)=f(x)+f(y)且当x>1时,f(x)>0.
(1)判断函数f(x)在其定义域(0,+∞)上的单调性并证明;
(2)解不等式f(x)+f(x﹣2)≤3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知a,b,c成等比数列,且 ![]() .
.
(Ⅰ)求角B的大小;
(Ⅱ)若b=3,求△ABC的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式(m﹣1)x2+(m﹣1)x+2>0的解集是R,则m的范围是( )
A.(1,9)
B.(﹣∞,1]∪(9,+∞)
C.[1,9)
D.(﹣∞,1)∪(9,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(n)=(1+ ![]() )n﹣n,其中n为正整数.
)n﹣n,其中n为正整数.
(1)求f(1),f(2),f(3)的值;
(2)猜想满足不等式f(n)<0的正整数n的范围,并用数学归纳法证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
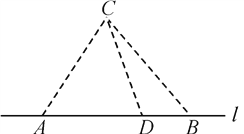
【题目】如图,在海岸线![]() 一侧
一侧![]() 处有一个美丽的小岛,某旅游公司为方便游客,在
处有一个美丽的小岛,某旅游公司为方便游客,在![]() 上设立了
上设立了![]() 两个报名点,满足
两个报名点,满足![]() 中任意两点间的距离为
中任意两点间的距离为![]() .公司拟按以下思路运作:先将
.公司拟按以下思路运作:先将![]() 两处游客分别乘车集中到
两处游客分别乘车集中到![]() 之间的中转点
之间的中转点![]() 处(点
处(点![]() 异于
异于![]() 两点),然后乘同一艘轮游轮前往
两点),然后乘同一艘轮游轮前往![]() 岛.据统计,每批游客
岛.据统计,每批游客![]() 处需发车2辆,
处需发车2辆, ![]() 处需发车4辆,每辆汽车每千米耗费
处需发车4辆,每辆汽车每千米耗费![]() 元,游轮每千米耗费
元,游轮每千米耗费![]() 元.(其中
元.(其中![]() 是正常数)设∠
是正常数)设∠![]() ,每批游客从各自报名点到
,每批游客从各自报名点到![]() 岛所需运输成本为
岛所需运输成本为![]() 元.
元.
(1) 写出![]() 关于
关于![]() 的函数表达式,并指出
的函数表达式,并指出![]() 的取值范围;
的取值范围;
(2) 问:中转点![]() 距离
距离![]() 处多远时,
处多远时, ![]() 最小?
最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com