
【题目】已知函数f(x)= ![]() +x.
+x.
(1)若函数f(x)的图象在(1,f(1))处的切线经过点(0,﹣1),求a的值;
(2)是否存在负整数a,使函数f(x)的极大值为正值?若存在,求出所有负整数a的值;若不存在,请说明理由;
(3)设a>0,求证:函数f(x)既有极大值,又有极小值.
【答案】
(1)解:∵ ![]() ,f′(1)=1,f(1)=ae+1
,f′(1)=1,f(1)=ae+1
∴函数f(x)在(1,f(1))处的切线方程为:y﹣(ae+1)=x﹣1,又直线过点(0,﹣1)
∴﹣1﹣(ae+1)=﹣1,解得:a=﹣ ![]()
(2)解:若a<0,∵ ![]() (x≠0),
(x≠0),
当x∈(﹣∞,0)时,f′(x)>0恒成立,函数在(﹣∞,0)上无极值;
当x∈(0,1)时,f′(x)>0恒成立,函数在(0,1)上无极值;
在x∈(1,+∞)时,令H(x)=aex(x﹣1)+x2,则H′(x)=(aex+2)x,
∵x∈(1,+∞),∴ex∈(e,+∞,)∵a为负整数∴a≤﹣1,∴aex≤ae≤﹣e
∴aex+2<0,∴H′(x)<0,∴H(x)在(1,+∞)上单调减,
又H(1)=1>0,H(2)=ae2+4≤﹣e2+4<0∴x0∈(1,2),使得H(x0)=0
且1<x<x0时,H′(x)>0,即f′(x)>0;x>x0时,H′(x)<0,即f′(x)<0;
∴f(x)在x0处取得极大值 ![]() (*)
(*)
又H(x0)=aex0(x0﹣1)+x02=0,∴ ![]() 代入(*)得:
代入(*)得:
![]() ,∴不存在负整数a满足条件
,∴不存在负整数a满足条件
(3)解:设g(x)=aex(x﹣1)+x2,则g′(x)=(aex+2)x,
因为a>0,所以,当x>0时,g′(x)>0,g(x)单调递增;
当x<0时,g′(x)<0,g(x)单调递减;故g(x)至多两个零点.
又g(0)=﹣a<0,g(1)=1>0,所以存在x1∈(0,1),使g(x1)=0
再由g(x)在(0,+∞)上单调递增知,
当x∈(0,x1)时,g(x)<0,故f′(x)= ![]() ,f(x)单调递减;
,f(x)单调递减;
当x∈(x2,+∞)时,g(x)>0,故故f′(x)= ![]() ,f(x)单调递增;
,f(x)单调递增;
所以函数f(x)在x1处取得极小值.
当x<0时,ex<1,且x﹣1<0,
所以g(x)=aex(x﹣1)+x2>a(x﹣1)+x2=x2+ax﹣a,
函数y=x2+ax﹣a是关于x的二次函数,必存在负实数t,使g(t)>0,又g(0)=﹣a<0,
故在(t,0)上存在x2,使g(x2)=0,
再由g(x)在(﹣∞,0)上单调递减知,
当x∈(﹣∞,x2)时,g(x)>0,故f′(x)= ![]() ,f(x)单调递增;
,f(x)单调递增;
当x∈(x2,0)时,g(x)<0,故f′(x)= ![]() ,f(x)单调递减;
,f(x)单调递减;
所以函数f(x)在x2处取得极大值.
综上,函数f(x)既有极大值,又有极小值
【解析】(1)第一步确定切点;第二步求斜率,即求曲线上该点的导数;第三步利用点斜式求出直线方程.(2)根据可导函数极值的定义,找到极值点,求出极值,当极大值为正数时,从而判定负整数是否存在;(3)利用单调性与极值的关系,求证:既存在极大值,有存在极小值.
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】(题文)已知平面内一动点P到点F(1,0)的距离与点P到y轴的距离的差等于1.
(1)求动点P的轨迹C的方程;
(2)过点F作两条斜率存在且互相垂直的直线l1,l2,设l1与轨迹C相交于点A,B,l2与轨迹C相交于点D,E,求![]() ·
·![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取顺序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() =
=![]() xi=9.97,s=
xi=9.97,s=![]() =
=![]() ≈0.212,
≈0.212,![]() ≈18.439,
≈18.439,![]() (xi﹣
(xi﹣![]() )(i﹣8.5)=﹣2.78,
)(i﹣8.5)=﹣2.78,
其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产
过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地
变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在(![]() ﹣3s,
﹣3s,![]() +3s)之外的零件,就认为这条生产线在这一天
+3s)之外的零件,就认为这条生产线在这一天
的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
①从这一天抽检的结果看,是否需对当天的生产过程进行检查?
②在(![]() ﹣3s,
﹣3s,![]() +3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的
+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的
均值与标准差.(精确到0.01)
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=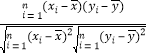 ,
,![]() ≈0.09.
≈0.09.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级3个班有10名学生在全国英语能力大赛中获奖,学生来源人数如表:
班别 | 高一(1)班 | 高一(2)班 | 高一(3)班 |
人数 | 3 | 6 | 1 |
若要求从10位同学中选出两位同学介绍学习经验,设其中来自高一(1)班的人数为ξ,求随机变量ξ的分布列及数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数![]() ,函数
,函数![]() .
.
(1) 若![]() ,求
,求![]() 的单调递减区间;
的单调递减区间;
(2) 若![]() 为奇函数,且关于
为奇函数,且关于![]() 的不等式
的不等式![]() 对所有的
对所有的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3) 当![]() 时,若方程
时,若方程![]() 有三个不相等的实数根
有三个不相等的实数根![]() 、
、![]() 、
、![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年存节期间,某服装超市举办了一次有奖促销活动,消费每超过600 元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种. 方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸到2个红球,则打6折;若摸到1个红球,则打7折;若没摸到红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了 600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com