
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左焦点为F,离心率为
=1(a>0,b>0)的左焦点为F,离心率为 ![]() .若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
.若经过F和P(0,4)两点的直线平行于双曲线的一条渐近线,则双曲线的方程为( )
A.![]()
=1
B.![]()
=1
C.![]()
=1
D.![]()
=1
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】如图,梯形ABCD内接于⊙O,AD∥BC,过点C作⊙O的切线,交BD的延长线于点P,交AD的延长线于点E. 
(1)求证:AB2=DEBC;
(2)若BD=9,AB=6,BC=9,求切线PC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin(2x+φ)+ ![]() cos(2x+φ)(0<φ<π)图象向左平移
cos(2x+φ)(0<φ<π)图象向左平移 ![]() 个单位后,得到函数的图象关于点(
个单位后,得到函数的图象关于点( ![]() ,0)对称,则函数g(x)=cos(x+φ)在[﹣
,0)对称,则函数g(x)=cos(x+φ)在[﹣ ![]() ,
, ![]() ]上的最小值是( )
]上的最小值是( )
A.﹣ ![]()
B.﹣ ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,双曲线 ![]() =1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .
=1(a>0,b>0)的右支与焦点为F的抛物线x2=2py(p>0)交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,焦距为2.(14分)
,焦距为2.(14分)
(Ⅰ)求椭圆E的方程.
(Ⅱ)如图,该直线l:y=k1x﹣ ![]() 交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为k2 , 且看k1k2=
交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为k2 , 且看k1k2= ![]() ,M是线段OC延长线上一点,且|MC|:|AB|=2:3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T,求∠SOT的最大值,并求取得最大值时直线l的斜率.
,M是线段OC延长线上一点,且|MC|:|AB|=2:3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T,求∠SOT的最大值,并求取得最大值时直线l的斜率.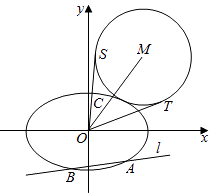
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20 , 接下来的两项是20 , 21 , 再接下来的三项是20 , 21 , 22 , 依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是( )
A.440
B.330
C.220
D.110
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是![]() .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①记“![]() ”为事件A,求事件A的概率;
”为事件A,求事件A的概率;
②在区间![]() 内任取2个实数
内任取2个实数![]() ,求事件“
,求事件“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com