考点:二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(1)以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,求出平面A1AC的法向量和平面ACB的法向量,由此能求出二面角A1-AC-B的大小.
(2)求出平面A1BD的法向量和平面 ABD的法向量,利用向量法能求出二面角A1-BD-A的大小.
解答:
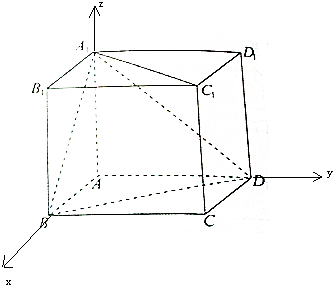
解:(1)以A为原点,AB为x轴,AD为y轴,
AA
1为z轴,建立空间直角坐标系,
A
1(0,0,a),A(0,0,0),C(a,a,0),
B(a,0,0),
=(a,a,0),
=(0,0,a),
=(a,0,0),
设平面A
1AC的法向量
=(x,y,z),
则
,
取x=1,得
=(1,-1,0),
又平面ACB的法向量
=(0,0,1),
设二面角A
1-AC-B的平面角为α,
cosα=
=0,∴α=90°,
∴二面角A
1-AC-B的大小为90°.
(2)D(0,a,0),
=(-a,a,0),
=(-a,0,a),
设平面A
1BD的法向量
=(x
1,y
1,z
1),
则
,取x
1=1,得
=(1,1,1),
又平面 ABD的法向量
=(0,0,1),
设二面角A
1-BD-A的大小为β,
cosβ=
=
=
,
∴二面角A
1-BD-A的大小为arccos
.
点评:本题主要考查直线与平面之间的平行、垂直等位置关系,空间向量、二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力.

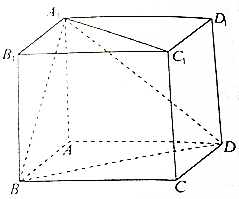 如图,正方体ABCD-A1B1C1D1的棱长为a,求:
如图,正方体ABCD-A1B1C1D1的棱长为a,求: 解:(1)以A为原点,AB为x轴,AD为y轴,
解:(1)以A为原点,AB为x轴,AD为y轴,

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案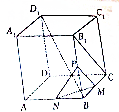 如图,在棱长为2的正方体ABCD一A1B1C1D1中,M为BC的中点,N为AB的中点,P为BB1的中点.
如图,在棱长为2的正方体ABCD一A1B1C1D1中,M为BC的中点,N为AB的中点,P为BB1的中点.