练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    直线ax+by+c=0（ab≠0）在两坐标轴上的截距相等，则a、b、c满足的条件是（ ）
    A．a=b
    B．|a|=|b|
    C．a=b且c=0
    D．c=0或c≠0且a=b
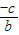
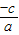
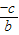
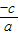
    【答案】分析：当c=0时，直线ax+by+c=0（ab≠0）过原点，在两坐标轴上的截距相等，当c≠0时，直线在两坐标轴上的截距分别为 和 ，由题意可得=，解得a=b，由此得出结论．
    解答：解：当c=0时，直线ax+by+c=0（ab≠0）过原点，在两坐标轴上的截距相等．
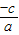
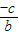
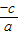
    当c≠0时，直线在两坐标轴上的截距分别为 和 ，由题意可得=，故a=b．
    综上，当c=0或c≠0且a=b时，直线ax+by+c=0（ab≠0）在两坐标轴上的截距相等，
    故选D．
    点评：本题主要考查直线的一般式方程，直线在两坐标轴上的截距的定义，体现了分类讨论的数学思想，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知直线Ax+By+C=0，
    （1）系数为什么值时，方程表示通过原点的直线；
    （2）系数满足什么关系时与坐标轴都相交；
    （3）系数满足什么条件时只与x轴相交；
    （4）系数满足什么条件时是x轴；
    （5）设P（x0，y0）为直线Ax+By+C=0上一点，证明：这条直线的方程可以写成A（x-x0）+B（y-y0）=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线Ax+By+C=0（其中A2+B2=C2，c≠0）与圆x2+y2=4交于M，N，O是坐标原点，则
    OM
    •
    ON
    =
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    流程图，如图所示，输出d的含义是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知ac＜0，bc＜0，则直线ax+by+c=0通过（　　）
    A、第一、二、三象限B、第一、二、四象限C、第一、三、四象限D、第二、三、四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若
    lim
    x→1
    x2+Ax+B
    x2-1
    =3    ，则直线Ax+By+C=0的倾斜角为
     
    ．

    查看答案和解析>>

    同步练习册答案