
����Ŀ����a��b��������������{cn}��n��N*���������£�c1=a��c2=b��������n��3��cn��cn��1+cn��2�������Լ��������{cn}�е�������ɼ���A��
��1����a=9��b=15�������A��
��2����k��1����dk=max{c2k �� c2k��1}��max{p��q}��ʾp��q�еĽϴ�ֵ������֤��dk+1��dk��
��3��֤������A����������д������A�е���С������
���𰸡�
��1���⣺����{cn}Ϊ��9��15��3��9��3��3��3��
�ʼ���A={9��15��3}��
��2��֤���������裬��n��3��cn��2��cn��1��������������cn��1+cn��2��ż����
�Ӷ�cn��1+cn��2�������Լ�� ![]() ��
��
����cn��max{cn��1��cn��2}�����ҽ���cn��1=cn��2ʱ�Ⱥų�����
���ԣ���k��1��c2k+1��max{c2k��c2k��1}=dk��
��c2k+2��max{c2k+1��c2k}��max{dk��dk}=dk��
����dk+1=max{c2k+2��c2k+1}��dk�����ҽ���c2k=c2k��1ʱ�Ⱥų�����
��3���ɣ�2��֪����n��3ʱ����cn��max{cn��1��cn��2}��
���Զ�n��3����cn��max{c1��c2}=max{a��b}��
��cn�����������Ҳ�����max{a��b}�������������ģ�
��������{cn}�еIJ�ͬ�������ģ�
���Լ���A��������
����A�е���С����a��b�����Լ��
����������1�������оٷ�д������{cn}���ü���A����2�������裬��n��3��cn��2 �� cn��1��������������cn��1+cn��2��ż�����Ӷ�cn��1+cn��2�������Լ�� ![]() ����ϲ���ʽ�����ʽ��н�𣻣�3��������ָԪ�صĸ����������ļ��ϣ��Ӷ�ȷ���𰸣�
����ϲ���ʽ�����ʽ��н�𣻣�3��������ָԪ�صĸ����������ļ��ϣ��Ӷ�ȷ���𰸣�
�����㾫����������Ĺؼ��������⼯�ϵı�ʾ����-�ض���ĸ�������֪ʶ�����բ���Ȼ���Է�����������������ʽ����������.���оٷ����Ѽ����е�Ԫ��һһ�оٳ�����д�ڴ������ڱ�ʾ����.����������{![]() |
|![]() �������}������
���е�����}������![]() Ϊ���ϵĴ���Ԫ��.��ͼʾ�����������Τ��ͼ����ʾ���ϣ�
Ϊ���ϵĴ���Ԫ��.��ͼʾ�����������Τ��ͼ����ʾ���ϣ�


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȷ����ĸ����ǣ� ��
�ٶ�������p��x��R��ʹ��x2+x��1��0����Vp��x��R������x2+x��1��0��
��p��q�ı�Ҫ�������������Vp�ǩVq�ij�ֲ���Ҫ������
�����⡰��x=y����sinx=siny�����������Ϊ�����⣻
�ܡ�m=��1���ǡ�ֱ��l1��mx+��2m��1��y+1=0��ֱ��l2��3x+my+3=0��ֱ���ij�Ҫ������
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}���������У�����lgan+1=|lgan��lgan��1|��n=2��3��4��������
��1����a1=2��a2=3����a3 �� a4 �� a5��ֵ��
��2����֤��������{an}�д���ak��k��N*��ʹ��lgak=0���ǡ�����{an}��������������1���ij�Ҫ������
��3����֤��������{an}��ak��k��N*����ʹ��1��ak��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��B��C��D�ĵ㹲�棬��CD=1��BC=2��AB=4����ABC=120�㣬cos��BDC= ![]() ��
�� 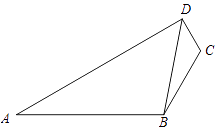
��1����sin��DBC��
��2����AD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣�
��![]() �У��ڽ�
�У��ڽ�![]() �Աߵı߳��ֱ���
�Աߵı߳��ֱ���![]() ����֪
����֪![]() ��
��![]() ��
��
��������![]() ���������
���������![]() ����
����![]() ��
��
��������![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �Ķ���Ϊ����ԭ��O������F��
�Ķ���Ϊ����ԭ��O������F��![]() ���������ϣ���
���������ϣ���![]() ��Բ
��Բ![]() ����.
����.
��������������![]() �ķ��̣�
�ķ��̣�
��������ֱ֪��![]() ��������
��������![]() ���ڵ�
���ڵ�![]() ������
������![]() ������ֱ��
������ֱ��![]() �����㣨0��1������
�����㣨0��1������ ![]() ����
����
���ж�����![]() ����٣���֤��.
����٣���֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A����![]() ��0����B��
��0����B��![]() ��0��������C��A��B����ľ���֮��ľ���ֵΪ2��
��0��������C��A��B����ľ���֮��ľ���ֵΪ2��
��1�����C�Ĺ켣���̣�
��2����C�Ĺ켣�뾭���㣨2��0����б��Ϊ1��ֱ�߽���D��E���㣬���߶�DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=sin2��x���أ�0������y=f��x����ͼ������ƽ�� ![]() ����λ���Ⱥ�������ͼ����ԭͼ���غϣ���ص���Сֵ���ڣ� ��
����λ���Ⱥ�������ͼ����ԭͼ���غϣ���ص���Сֵ���ڣ� ��
A.2
B.4
C.6
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
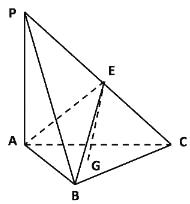
����Ŀ����ͼ��������P��ABC�У�ƽ��PAC��ƽ��ABC��PA��AC��AB=BC=CA=AP=2��G�ǡ�ABC���ģ�E���߶�PC��һ�㣬��CE=��CP��
��1����EG��ƽ��PABʱ��������ֵ��
��2����ֱ��CP��ƽ��ABE���ɽǵ�����ֵΪ![]() ʱ��������ֵ��
ʱ��������ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com