
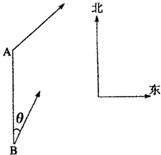
 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15 海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东θ(tanθ=
海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东θ(tanθ= )的方向作匀速直线航行,速度为10
)的方向作匀速直线航行,速度为10 海里/小时.
海里/小时.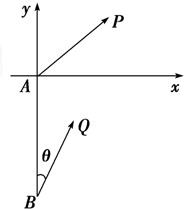 解:以A为原点,BA所在直线为y轴建立如图所示的平面直角坐标系.
解:以A为原点,BA所在直线为y轴建立如图所示的平面直角坐标系.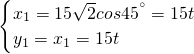
 可得,
可得, ,sinθ=
,sinθ= ,
,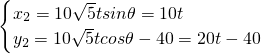
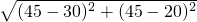 =
=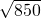 =5
=5 .
. 海里.
海里.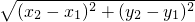
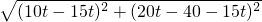
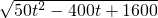 =
=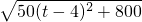 ≥20
≥20 ,
, .
. 海里.
海里. 海里,所以两船在航行中不会相遇
海里,所以两船在航行中不会相遇 可求得cosθ和sinθ的值,进而表示出x2和y2,令t=3,则P,Q两点坐标可得,进而根据两点间的距离求得PQ的值,即出发后3小时两船相距的距离.
可求得cosθ和sinθ的值,进而表示出x2和y2,令t=3,则P,Q两点坐标可得,进而根据两点间的距离求得PQ的值,即出发后3小时两船相距的距离. 海里.
海里. 海里,推断出两船不可能相遇.
海里,推断出两船不可能相遇.

科目:高中数学 来源: 题型:
 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15| 2 |
| 1 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15
如图所示,甲船由A岛出发向北偏东45°的方向作匀速直线航行,速度为15| 2 |
| 1 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省开封市高三模拟考试理科数学 题型:解答题
(本小题满分12分)
如图所示,甲船由A岛出发向北偏东 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为 海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东
海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东 的方向作匀速直线航行,速度为
的方向作匀速直线航行,速度为 海里/小时。
海里/小时。

(1)若两船能相遇,求 。
。
(2)当 时,求两船出发后多长时间距离最近,最近距离为多少海里?
时,求两船出发后多长时间距离最近,最近距离为多少海里?
查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:3 三角函数、解三角形 质量检测(1)(解析版) 题型:解答题
 海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东θ(tanθ=
海里/小时,在甲船从A岛出发的同时,乙船从A岛正南40海里处的B岛出发,朝北偏东θ(tanθ= )的方向作匀速直线航行,速度为10
)的方向作匀速直线航行,速度为10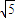 海里/小时.
海里/小时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com