
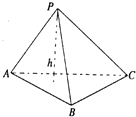
 在Rt△ABC中,两直角边分别为a,b,设h为斜边上的高,则$\frac{1}{h^2}$=$\frac{1}{a^2}$+$\frac{1}{b^2}$,类比此性质,如图,在四面体P-ABC 中,若PA,PB,PC两两垂直,且长度分别为a,b,c,设棱锥底面ABC上的高为h,则得到的正确结论为$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$.
在Rt△ABC中,两直角边分别为a,b,设h为斜边上的高,则$\frac{1}{h^2}$=$\frac{1}{a^2}$+$\frac{1}{b^2}$,类比此性质,如图,在四面体P-ABC 中,若PA,PB,PC两两垂直,且长度分别为a,b,c,设棱锥底面ABC上的高为h,则得到的正确结论为$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$. 分析 立体几何中的类比推理主要是基本元素之间的类比:平面?空间,点?点或直线,直线?直线或平面,平面图形?平面图形或立体图形,故本题由平面上的直角三角形中的边与高的关系式类比立体中两两垂直的棱的三棱锥中边与高的关系即可.
解答 解:∵PA、PB、PC两两互相垂直,
∴PA⊥平面PBC.
设PD在平面PBC内部,且PD⊥BC,
由已知有:PD=$\frac{bc}{\sqrt{{b}^{2}+{c}^{2}}}$,h=PO=$\frac{a•PD}{\sqrt{{a}^{2}+P{D}^{2}}}$,
∴h2=$\frac{{a}^{2}{b}^{2}{c}^{2}}{{a}^{2}{b}^{2}+{b}^{2}{c}^{2}+{c}^{2}{a}^{2}}$,即 $\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$.
故答案为:$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$.
点评 类比推理是指依据两类数学对象的相似性,将已知的一类数学对象的性质类比迁移到另一类数学对象上去.其思维过程大致是:观察、比较 联想、类推 猜测新的结论.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∉∁RQ,x0∈Q | B. | ?x0∈∁RQ,x0∈Q | C. | ?x∉∁RQ,x∉Q | D. | ?x∈∁RQ,x∉Q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
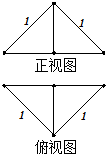 把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.
把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{30}$ | B. | $\frac{7}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{7}{30}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,-1) | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com