
【题目】设函数![]() 的定义域为
的定义域为![]() ,对于区间
,对于区间![]() ,若
,若![]() 满足
满足![]() ,则称区间
,则称区间![]() 为函数
为函数![]() 的
的![]() 区间.
区间.
(1)证明:区间![]() 是函数
是函数![]() 的
的![]() 区间;
区间;
(2)若区间![]() 是函数
是函数![]() 的
的![]() 区间,求实数
区间,求实数![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在区间
在区间![]() 上的图象连续不断,且在
上的图象连续不断,且在![]() 上仅有
上仅有![]() 个零点,证明:区间
个零点,证明:区间![]() 不是函数
不是函数![]() 的
的![]() 区间.
区间.
【答案】(1)证明见解析(2)![]() (3)证明见解析
(3)证明见解析
【解析】
(1)根据题中定义代入验证即可证出;
(2)根据题中的新定义可得![]() ,由
,由![]() 在
在![]() 上单调递减,可得
上单调递减,可得![]() ,只需
,只需![]() 即可求解.
即可求解.
(3)利用零点存在定理可得函数![]() 在
在![]() 上至少存在两个零点,由题意可得函数
上至少存在两个零点,由题意可得函数![]() 在
在![]() 上不存在零点,由
上不存在零点,由![]() ,可得
,可得![]() ,
,![]() ,从而可得
,从而可得![]() ,结合定义即可求解.
,结合定义即可求解.
(1)设![]() ,若
,若![]() ,则
,则![]()
所以![]() ,
,![]() ,
,
取![]() ,满足定义
,满足定义
所以区间![]() 是函数
是函数![]() 的
的![]() 区间,
区间,
(2)因为区间![]() 是函数
是函数![]() 的
的![]() 区间,
区间,
所以![]() 使得
使得![]() ,
,
因为![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,
,![]()
所以![]() ,
,![]() ,
,![]() ,
,
故所求实数![]() 的取值范围为
的取值范围为![]() ,
,
(3)因为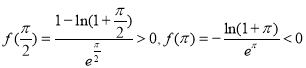 ,
,
所以![]() 在
在![]() 上存在零点,
上存在零点,
又因为![]() ,
,
所以函数![]() 在
在![]() 上至少存在两个零点.
上至少存在两个零点.
因为函数![]() 在区间
在区间![]() 上仅有
上仅有![]() 个零点.
个零点.
所以![]() 在
在![]() 上不存在零点.
上不存在零点.
又因为![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
即因此不存在![]() 满足
满足![]() ,
,
所以区间![]() 不是函数
不是函数![]() 的
的![]() 区间.
区间.


科目:高中数学 来源: 题型:
【题目】已知![]() ,直线
,直线![]() 与函数
与函数![]() 的图象在
的图象在![]() 处相切,设
处相切,设![]() ,若在区间[1,2]上,不等式
,若在区间[1,2]上,不等式![]() 恒成立.则实数m( )
恒成立.则实数m( )
A. 有最大值![]() B. 有最大值e C. 有最小值e D. 有最小值
B. 有最大值e C. 有最小值e D. 有最小值![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在非零常数![]() ,对于函数
,对于函数![]() 定义域上的任意
定义域上的任意![]() ,都有
,都有![]() 成立,那么称函数为“
成立,那么称函数为“![]() 函数”.
函数”.
(Ⅰ)若![]() ,
,![]() ,试判断函数
,试判断函数![]() 和
和![]() 是否是“
是否是“![]() 函数”?若是,请证明:若不是,主说明理由:
函数”?若是,请证明:若不是,主说明理由:
(Ⅱ)求证:若![]() 是单调函数,则它是“
是单调函数,则它是“![]() 函数”;
函数”;
(Ⅲ)若函数![]() 是“
是“![]() 函数”,求实数
函数”,求实数![]() 满足的条件.
满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
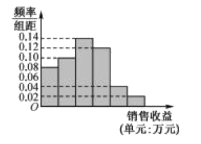
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司在若干地区各投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 3 | 7 |
由表中的数据显示,![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.(参考公式:
的回归直线方程.(参考公式: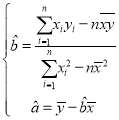 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的《车辆驾驶人员血液、呼吸酒精含量阀值与检验》国家标准,新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升,小于80毫克/百毫克升为饮酒驾车,血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车,经过反复试验,喝1瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下:
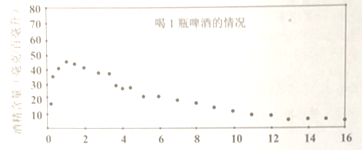
该函数模型如下:
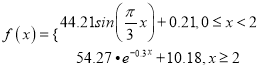
根据上述条件,回答以下问题:
(1)试计算喝1瓶啤酒后多少小时血液中的酒精含量达到最大值?最大值是多少?
(2)试计算喝1瓶啤酒后多少小时后才可以驾车?(时间以整小时计算)
(参数数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年东京夏季奥运会将设置
年东京夏季奥运会将设置![]() 米男女混合泳接力这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员比赛,按照仰泳
米男女混合泳接力这一新的比赛项目,比赛的规则是:每个参赛国家派出2男2女共计4名运动员比赛,按照仰泳![]() 蛙泳
蛙泳![]() 蝶泳
蝶泳![]() 自由泳的接力顺序,每种泳姿
自由泳的接力顺序,每种泳姿![]() 米且由一名运动员完成, 每个运动员都要出场. 现在中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或自由泳,剩下的男女各一名运动员则四种泳姿都可以上,那么中国队共有( )种兵布阵的方式.
米且由一名运动员完成, 每个运动员都要出场. 现在中国队确定了备战该项目的4名运动员名单,其中女运动员甲只能承担仰泳或者自由泳,男运动员乙只能承担蝶泳或自由泳,剩下的男女各一名运动员则四种泳姿都可以上,那么中国队共有( )种兵布阵的方式.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线平行于直线
处的切线平行于直线![]() ,求实数a的值;
,求实数a的值;
(Ⅱ)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(Ⅲ)在(Ⅰ)的条件下,若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com