
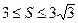 ,且
,且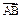 ·
·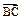 =6,
=6,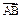 与
与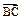 的夹角为
的夹角为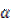 。(1)求
。(1)求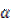 的取值范围;
的取值范围;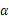 )=sin2
)=sin2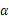 +2sin
+2sin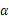 cos
cos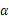 +3cos2
+3cos2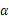 ,求f(
,求f(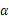 )的最小值,并指出取得最小值时的
)的最小值,并指出取得最小值时的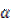 。
。科目:高中数学 来源:不详 题型:解答题
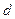 ;②A点处对M、N两点的俯角分别为
;②A点处对M、N两点的俯角分别为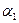 和
和 ;B点处对M、N两点的俯角分别为
;B点处对M、N两点的俯角分别为 和
和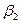 ;请同学们在示意图中标出这四个俯角并用文字和公式写出计算M,N间的距离的步骤.
;请同学们在示意图中标出这四个俯角并用文字和公式写出计算M,N间的距离的步骤.
 (2)在△ABC 中,若AB=2,AC=2BC,求△ABC面积的最大值.
(2)在△ABC 中,若AB=2,AC=2BC,求△ABC面积的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
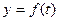 是某港口水的深度
是某港口水的深度 (米)关于时间
(米)关于时间 (时)的函数,其中
(时)的函数,其中 ,下表是该港口某一天从0时至24时记录的时间
,下表是该港口某一天从0时至24时记录的时间 与水深
与水深 的关系:
的关系: | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
 | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
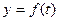 可以近似看成
可以近似看成 的图象,下面的函数中最能近似地表示表中数据对应关系的函数是( )
的图象,下面的函数中最能近似地表示表中数据对应关系的函数是( )A. , , | B. , , |
C. , , | D. , , |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
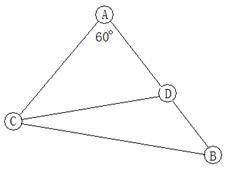
 海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离为 海里.
海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘轮船之间的距离为 海里. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com