
【题目】已知函数![]() ,
,
(1)试证明函数![]() 是偶函数;
是偶函数;
(2)画出![]() 的图象;(要求先用铅笔画出草图,再用黑色签字笔描摹,否则不给分)
的图象;(要求先用铅笔画出草图,再用黑色签字笔描摹,否则不给分)
(3)请根据图象指出函数![]() 的单调递增区间与单调递减区间;(不必证明)
的单调递增区间与单调递减区间;(不必证明)
(4)当实数![]() 取不同的值时,讨论关于
取不同的值时,讨论关于![]() 的方程
的方程![]() 的实根的个数;(不必求出方程的解)
的实根的个数;(不必求出方程的解)
【答案】(1)详见解析(2)详见解析(3)增区间![]() 减区间
减区间![]() (4)①当
(4)①当![]() 时,方程无实数根;②当
时,方程无实数根;②当![]() 或
或![]() 时,方程有两个实数根;③当
时,方程有两个实数根;③当![]() 时,方程有三个实数根;④当
时,方程有三个实数根;④当![]() 时,方程有四个实数根
时,方程有四个实数根
【解析】
试题分析:(1)根据函数的定义域为R,关于原点对称,且满足f(-x)=f(x),可得函数 f(x)是偶函数.(2)先去绝对值,然后根据二次函数、分段函数图象的画法画出函数f(x)的图象.(3)通过图象即可求得f(x)的单调递增和递减区间;(4)通过图象即可得到k的取值和对应的原方程实根的个数
试题解析:(1)![]() 的定义域为
的定义域为![]() ,且
,且
![]()
![]()
故![]() 为偶函数;
为偶函数;
(2)如图
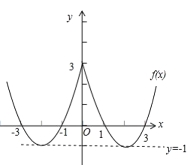
(3)递增区间有:![]()
递减区间有:![]()
(4)根据图象可知,
①当![]() 时,方程无实数根;
时,方程无实数根;
②当![]() 或
或![]() 时,方程有两个实数根;
时,方程有两个实数根;
③当![]() 时,方程有三个实数根;
时,方程有三个实数根;
④当![]() 时,方程有四个实数根;
时,方程有四个实数根;


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】某校高一年级学生身体素质体能测试的成绩(百分制)分布在![]() 内,同时为了了解学生爱好数学的情况,从中随机抽取了
内,同时为了了解学生爱好数学的情况,从中随机抽取了![]() 名学生,这
名学生,这![]() 名学生体能测试成绩的频率分布直方图如图所示,各分数段的“爱好数学”的人数情况如表所示.
名学生体能测试成绩的频率分布直方图如图所示,各分数段的“爱好数学”的人数情况如表所示.

(1)求![]() 的值;
的值;
(2)用分层抽样的方法,从体能成绩在![]() 的“爱好数学”学生中随机抽取6人参加某项活动,现从6人中随机选取2人担任领队,求两名领队中恰有1人体能成绩在
的“爱好数学”学生中随机抽取6人参加某项活动,现从6人中随机选取2人担任领队,求两名领队中恰有1人体能成绩在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若有一个企业,70%的员工年收入1万元,25%的员工年收入3万元,5%的员工年收入11万元,则该企业员工的年收入的平均数是________万元,中位数是________万元,众数是________万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系中,已知直线![]() 过点
过点![]() ,倾斜角
,倾斜角![]() ,再以原点为极点,
,再以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类比平面几何中的命题:“垂直于同一直线的两条直线平行”,在立体几何中,可以得到命题“__________”,这个类比命题的真假性是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)求![]() 的极值;
的极值;
(2)设![]() ≤
≤![]() ,记
,记![]() 在
在![]() 上的最大值为
上的最大值为![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)设函数![]() (
(![]() 为常数),若使
为常数),若使![]() ≤
≤![]() ≤
≤![]() 在
在![]() 上恒成立的实数
上恒成立的实数![]() 有且只有一个,求实数
有且只有一个,求实数![]() 和
和![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com