
【题目】已知![]() ,函数
,函数![]() 有两个不同的零点
有两个不同的零点![]()
![]() .
.
(I)证明:![]() ;
;
(Ⅱ)证明:![]() .
.
【答案】(I)证明见解析(Ⅱ)证明见解析
【解析】
(I)分离参数,构造函数![]() ,利用导数讨论
,利用导数讨论![]() 的单调性以及最值,根据直线
的单调性以及最值,根据直线![]() 与
与![]() 有两个交点,即可求得参数的范围;
有两个交点,即可求得参数的范围;
(Ⅱ)先证明![]() ,再证明
,再证明![]() 成立即可.
成立即可.
证明:(I)由![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减.
单调递减.
因为![]() 有两个不同的零点,故
有两个不同的零点,故![]() ,即
,即![]() .
.
若![]() ,则当
,则当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上无零点,
上无零点,
![]() 在
在![]() 上至多一个零点,与题设矛盾,故
上至多一个零点,与题设矛盾,故![]() .
.
(Ⅱ)(1)一方面,先证明![]() 成立:
成立:
设![]() ,由(I)可知
,由(I)可知![]() .
.
构造函数![]() ,
,
所以![]() .
.
所以当![]() 时,
时,![]() ,
,![]() 递增,
递增,
所以![]() ,即
,即![]() .
.
因为![]() ,所以
,所以![]() ,
,
即![]() .
.
又因为![]()
![]() ,且
,且![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() .
.
(2)另一方面,要证明![]() 成立,
成立,
只需证明![]() 成立,
成立,
由![]() 知
知![]() ,
,
故只需证明![]() ,即
,即![]() 成立
成立
![]() 等价于
等价于![]() ,
,
因为![]() ,所以只需证明
,所以只需证明![]() ,
,
即![]() 成立.
成立.
设函数![]() ,则
,则![]() ,
,
当![]() 时
时![]() ,
,![]() 单调递减,
单调递减,
于是![]() ,故
,故![]() 成立
成立
综上所述:![]() .
.


科目:高中数学 来源: 题型:
【题目】炼钢是一个氧化降碳的过程,由于钢水含碳量的多少直接影响冶炼时间的长短,因此必须掌握钢水含碳量和冶炼时间的关系.现已测得炉料熔化完毕时钢水的含碳量![]() 与冶炼时间
与冶炼时间![]() (从炉料熔化完毕到出钢的时间)的一组数据,如下表所示:
(从炉料熔化完毕到出钢的时间)的一组数据,如下表所示:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
| 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
| 10400 | 36000 | 39900 | 32745 | 22785 | 18090 | 25500 | 39155 | 47940 | 15125 |
(1)据统计表明,![]() 与
与![]() 之间具有线性相关关系,请用相关系数
之间具有线性相关关系,请用相关系数![]() 加以说明(
加以说明(![]()
![]() ,则认为
,则认为![]() 与
与![]() 有较强的线性相关关系,否则认为没有较强的线性相关关系,
有较强的线性相关关系,否则认为没有较强的线性相关关系,![]() 精确到0.001);
精确到0.001);
(2)建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)根据(2)中的结论,预测钢水含碳量为160个0.01%的冶炼时间.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ,
,
![]() ,相关系数
,相关系数
参考数据: ,
,
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援,现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.

(1)求出易倒伏玉米茎高的中位数![]() ;
;
(2)根据茎叶图的数据,完成下面的列联表:
抗倒伏 | 易倒伏 | |
矮茎 | ||
高茎 |
(3)根据(2)中的列联表,是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
附: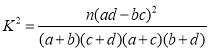 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 为椭圆
为椭圆![]() 上任意一点,且
上任意一点,且![]() 的最小值为0.
的最小值为0.
(1)求椭圆![]() 的方程;
的方程;
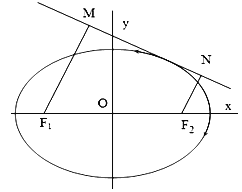
(2)如图,动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,点
有且仅有一个公共点,点![]() ,
,![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() ,
,![]() ,求四边形
,求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )



A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com