
【题目】为减少空气污染,某市鼓励居民用电(减少燃气或燃煤),采用分段计费的方法计算电费.每月用电不超过100度时,按每度0.57元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.5元计算.
(1)设月用电x度时,应交电费y元,写出y关于x的函数关系式;
(2)小明家第一季度缴纳电费情况如下:问小明家第一季度共用电多少度?
月份 | 一月 | 二月 | 三月 | 合计 |
交费金额 | 76元 | 63元 | 45.6元 | 184.6元 |
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (x﹣2)的定义域为集合A,函数
(x﹣2)的定义域为集合A,函数![]() 的值域为集合B.
的值域为集合B.
(1)求A∪B;
(2)若集合C={x|a≤x≤3a﹣1},且B∩C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分10分)
已知椭圆![]()
![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,离心率
,离心率![]() .过
.过![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() .求证:以
.求证:以![]() 为直径的圆恒过一定点
为直径的圆恒过一定点![]() .并求出点
.并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程是
的方程是![]() ,双曲线
,双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() 的左右顶点,而
的左右顶点,而![]() 的左右顶点分别是
的左右顶点分别是![]() 的左右焦点.
的左右焦点.
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 与双曲线
与双曲线![]() 恒有两个不同的交点,且
恒有两个不同的交点,且![]() 与
与![]() 的两个交点A和B满足
的两个交点A和B满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是[0,1]上的不减函数,即对于0≤x1≤x2≤1有f(x1)≤f(x2),且满足(1)f(0)=0;(2)f( ![]() )=
)= ![]() f(x);(3)f(1﹣x)=1﹣f(x),则f(
f(x);(3)f(1﹣x)=1﹣f(x),则f( ![]() )=( )
)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
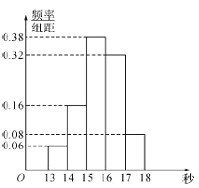
(1)根据频率分布直方图,估计这50名学生百米测试成绩的中位数和平均值(精确到![]() );
);
(2)若从第一、五组中随机取出两个成绩,列举所有选取方法,并求这两个成绩的差的绝对值大于1的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com