
【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成A,B两组,每组20人,A组群众给第一阶段的创文工作评分,B组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如图茎叶图:

![]() 根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度
根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度![]() 不要求计算出具体值,给出结论即可
不要求计算出具体值,给出结论即可![]() ;
;
![]() 根据群众的评分将满意度从低到高分为三个等级:
根据群众的评分将满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
![]() 由频率估计概率,判断该市开展创文工作以来哪个阶段的民众满意率高?说明理由.
由频率估计概率,判断该市开展创文工作以来哪个阶段的民众满意率高?说明理由.
![]() 完成下面的列联表,并根据列联表判断是否有
完成下面的列联表,并根据列联表判断是否有![]() 的把握认为民众对两个阶段创文工作的满意度存在差异?
的把握认为民众对两个阶段创文工作的满意度存在差异?
低于70分 | 不低于70分 | |
第一阶段 | ||
第二阶段 |
附:![]()
|
|
|
|
k |
|
|
|
【答案】(1)见解析;(2)①第二阶段更高;②有![]() 的把握.
的把握.
【解析】
(1)根据茎叶图看出![]() 组群众给第二阶段创文工作满意度评分的平均值高于
组群众给第二阶段创文工作满意度评分的平均值高于![]() 组群众的平均值,且给分相对于
组群众的平均值,且给分相对于![]() 组更集中些;
组更集中些;
(2)①记![]() 表示事件“第一阶段创文工作满意度评分不低于
表示事件“第一阶段创文工作满意度评分不低于![]() 分”,
分”,![]() 表示事件“第二阶段创文工作满意度评分不低于
表示事件“第二阶段创文工作满意度评分不低于![]() 分”,由茎叶图,利用频率估计概率,计算
分”,由茎叶图,利用频率估计概率,计算![]() 、
、![]() 的值,比较大小即可;②填写列联表,计算
的值,比较大小即可;②填写列联表,计算![]() ,对照临界值得出结论.
,对照临界值得出结论.
(1)根据茎叶图看出,![]() 组群众给第二阶段创文工作满意度评分的“叶”分布在“茎”的
组群众给第二阶段创文工作满意度评分的“叶”分布在“茎”的![]() 上,也相对集中在峰值的附近
上,也相对集中在峰值的附近
所以![]() 组给第二阶段创文工作满意度评分的平均值高于
组给第二阶段创文工作满意度评分的平均值高于![]() 组群众第一阶段创文工作满意度评分的平均值,给分相对于
组群众第一阶段创文工作满意度评分的平均值,给分相对于![]() 组更集中些
组更集中些
(2)①记![]() 表示事件“第一阶段创文工作满意度评分不低于
表示事件“第一阶段创文工作满意度评分不低于![]() 分”,
分”,![]() 表示事件“第二阶段创文工作满意度评分不低于
表示事件“第二阶段创文工作满意度评分不低于![]() 分”
分”
由茎叶图可知,给第一阶段评分的![]() 名
名![]() 组群众中,评分不低于
组群众中,评分不低于![]() 分的有
分的有![]() 人
人
给第二阶段评分的![]() 名
名![]() 组群众中,评分不低于
组群众中,评分不低于![]() 分的有
分的有![]() 人,则由频率估计概率:
人,则由频率估计概率:
![]() ,
,![]() ,则
,则![]()
所以该市开展创文工作以来第二阶段的民众满意率比第一阶段的高
②填写列联表如下,
低于 | 不低于 | |
第一阶段 |
|
|
第二阶段 |
|
|
计算![]()
所以有![]() 的把握认为民众对两个阶段创文工作的满意度存在差异
的把握认为民众对两个阶段创文工作的满意度存在差异


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,若椭圆C的离心率为
两点,若椭圆C的离心率为![]() ,
,![]() 的周长为8.
的周长为8.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知直线![]() 与椭圆C交于
与椭圆C交于![]() 两点,是否存在实数k使得以
两点,是否存在实数k使得以![]() 为直径的圆恰好经过坐标原点?若存在,求出k的值;若不存在,请说明理由.
为直径的圆恰好经过坐标原点?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面四边形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起至
折起至![]() ,使平面
,使平面![]() ,则四面体
,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
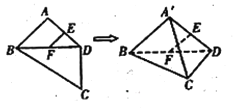
A.![]() 平面
平面![]()
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在原点
的顶点在原点![]() ,对称轴是
,对称轴是![]() 轴,且过点
轴,且过点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知斜率为![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,且与曲线
,且与曲线![]() 相切于点
相切于点![]() ,点
,点![]() 在曲线
在曲线![]() 上,且直线
上,且直线![]() 轴,
轴, ![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,判断点
,判断点![]() 是否共线,并说明理由.
是否共线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】惠州市某学校需要从甲、乙两名学生中选1人参加数学竞赛,抽取了近期两人5次数学考试的分数,统计结果如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲 | 80 | 85 | 71 | 92 | 87 |
乙 | 90 | 76 | 75 | 92 | 82 |
(1)若从甲、乙两人中选出1人参加数学竞赛,你认为选谁合适?请说明理由.
(2)若数学竞赛分初赛和复赛,在初赛中答题方案如下:
每人从5道备选题中随机抽取3道作答,若至少答对其中2道,则可参加复赛,否则被淘汰.假设被选中参赛的学生只会5道备选题中的3道,求该学生能进人复赛的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年数学竞赛邀请了一位来自![]() 星球的选手参加填空题比赛,共10道题目,这位选手做题有一个古怪的习惯:先从最后一题(第10题)开始往前看,凡是遇到会的题目就作答,遇到不会的题目先跳过(允许跳过所有的题目),一直看到第1题,然后从第1题开始往后看,凡是遇到先前未答的题目就随便写个答案,遇到先前已答得题目则跳过(例如,他可以按照9、8、7、4、3、2、1、5、6、10的次序答题),这样所有题目均有作答,则这位选手可能的答题次序有______种.
星球的选手参加填空题比赛,共10道题目,这位选手做题有一个古怪的习惯:先从最后一题(第10题)开始往前看,凡是遇到会的题目就作答,遇到不会的题目先跳过(允许跳过所有的题目),一直看到第1题,然后从第1题开始往后看,凡是遇到先前未答的题目就随便写个答案,遇到先前已答得题目则跳过(例如,他可以按照9、8、7、4、3、2、1、5、6、10的次序答题),这样所有题目均有作答,则这位选手可能的答题次序有______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的侧面
的侧面![]() 是平行四边形,
是平行四边形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分别是
分别是![]() 的中点.
的中点.

(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,![]() ,
,![]() ,
,![]() ,M是棱PC上一点,且
,M是棱PC上一点,且![]() ,
,![]() 平面MBD.
平面MBD.
(1)求实数λ的值;
(2)若平面![]() 平面ABCD,
平面ABCD,![]() 为等边三角形,且三棱锥P-MBD的体积为2,求PA的长.
为等边三角形,且三棱锥P-MBD的体积为2,求PA的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,等腰梯形ABCD中,AB∥CD,AD=AB=BC=1,CD=2,E为CD中点,AE与BD交于点O,将△ADE沿AE折起,使点D到达点P的位置(P平面ABCE).
(Ⅰ)证明:平面POB⊥平面ABCE;
(Ⅱ)若直线PB与平面ABCE所成的角为![]() ,求二面角A-PE-C的余弦值.
,求二面角A-PE-C的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com