
【题目】已知函数![]() .
.
(1)当![]() ,
, ![]() 取一切非负实数时,若
取一切非负实数时,若![]() ,求
,求![]() 的范围;
的范围;
(2)若函数![]() 存在极大值
存在极大值![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)当![]() 时,
时, ![]() ,原题分离参数得
,原题分离参数得![]() 恒成立,右边求导求出其最大值即可;(2)对其求导
恒成立,右边求导求出其最大值即可;(2)对其求导![]() ,当
,当![]() 时,
时, ![]() 在
在![]() 上为单增函数,无极大值;当
上为单增函数,无极大值;当![]() 时,
时, ![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,其中
上为减函数,其中![]() 满足
满足![]() ,故可得极大值
,故可得极大值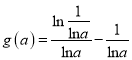 ,令
,令![]() ,得
,得![]() ,对其求导可得其最小值.
,对其求导可得其最小值.
试题解析:(1)当![]() 时,
时, ![]() ,
, ![]() 恒成立等价于
恒成立等价于![]() 恒成立,令
恒成立,令![]() ,
, ![]() ,
, ![]() ,当
,当![]() 时,
时, ![]() 恒成立,即
恒成立,即![]() 在
在![]() 内单调递减,故
内单调递减,故![]() ,可得
,可得![]() 在
在![]() 内单调递减,故
内单调递减,故![]() .
.
(2)![]() ,
,
①当![]() 时,
时, ![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上为单增函数,无极大值;
上为单增函数,无极大值;
②当![]() 时,设方程
时,设方程![]() 的根为
的根为![]() ,则有
,则有![]() ,即
,即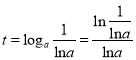 ,所以
,所以![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,所以
上为减函数,所以![]() 的极大值为
的极大值为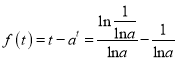 ,即
,即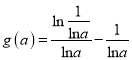 ,因为
,因为![]() ,所以
,所以![]() ,令
,令![]() 则
则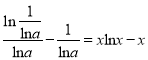 ,
,
设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,所以
上为增函数,所以![]() 得最小值为
得最小值为![]() ,即
,即![]() 的最小值为-1,此时
的最小值为-1,此时![]() .
.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线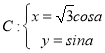 (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立的极坐标系中,直线的极坐标方程为:
轴的非负半轴为极轴建立的极坐标系中,直线的极坐标方程为: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线的直角坐标方程;
的普通方程和直线的直角坐标方程;
(Ⅱ)过点![]() 且与直线平行的直线
且与直线平行的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,求点
两点,求点![]() 到
到![]() ,
, ![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() .
.
(Ⅰ)若![]() 为等边三角形,求椭圆
为等边三角形,求椭圆![]() 的方程;
的方程;
(Ⅱ)若椭圆![]() 的短轴长为
的短轴长为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() .
.
(Ⅰ)若![]() 为等边三角形,求椭圆
为等边三角形,求椭圆![]() 的方程;
的方程;
(Ⅱ)若椭圆![]() 的短轴长为
的短轴长为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足f(0)=2和f(x+1)﹣f(x)=2x﹣1对任意实数x都成立.
(1)求函数f(x)的解析式;
(2)当t∈[﹣1,3]时,求y=f(2t)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
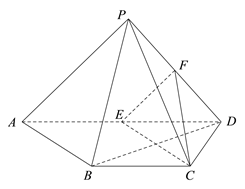
【题目】如图,四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() //
// ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为
线段![]() ,
, ![]() 的中点.
的中点.
(Ⅰ)求证: ![]() //平面
//平面![]() ;
;
(Ⅱ)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)写出三棱锥![]() 与三棱锥
与三棱锥![]() 的体积之比.(结论不要求证明)
的体积之比.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)为选拔选手参加“中国汉字听写大会”,某中学举行了一次“汉字听写大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() ,
, ![]() 的数据).
的数据).

(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 、
、![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国汉字听写大会”,求所抽取的2名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com