
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,△
的中点,△![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.

(1)若![]() ∥平面
∥平面![]() ,求
,求![]() ;
;
(2)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:(1) 取![]() 中点为
中点为![]() ,连结
,连结![]() ,根据条件
,根据条件![]() ∥平面
∥平面![]() ,又有平面
,又有平面![]() 平面
平面![]() ,这样根据线面平行的性质定理,可得
,这样根据线面平行的性质定理,可得![]() ,这样根据平行线的比例可得
,这样根据平行线的比例可得![]() 的值;
的值;
(2)如图,通过割补法将几何体![]() 补成三棱柱
补成三棱柱![]() ,那么所求几何体
,那么所求几何体![]() 的体积就是
的体积就是![]() ,然后再用大的三棱柱的体积减小部分的体积,就是剩下的几何体的体积,再求其比值.
,然后再用大的三棱柱的体积减小部分的体积,就是剩下的几何体的体积,再求其比值.
试题解析:取![]() 中点为
中点为![]() ,连结
,连结![]() ,
,
∵![]() 分别为
分别为![]() 中点
中点
∴![]() ∥
∥![]() ∥
∥![]() ,∴
,∴![]() 四点共面,
四点共面,
且平面![]() 平面
平面![]()
![]()
又![]() 平面
平面![]() ,且
,且![]() ∥平面
∥平面![]()
∴![]() ∥
∥![]()
∵![]() 为
为![]() 的中点,
的中点,
∴![]() 是
是![]() 的中点,
的中点,
∴![]() .
.

(2)因为三棱柱![]() 为直三棱柱,
为直三棱柱,![]() 平面
平面![]() ,
,
又![]() ,则
,则![]() 平面
平面![]()
设![]() ,又三角形
,又三角形![]() 是等腰三角形,所以
是等腰三角形,所以![]() .
.
如图,将几何体![]() 补成三棱柱
补成三棱柱![]()
∴几何体![]() 的体积为:
的体积为:
![]()
又直三棱柱![]() 体积为:
体积为:![]()
故剩余的几何体棱台![]() 的体积为:
的体积为:![]()
∴较小部分的体积与较大部分体积之比为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如下.

(1)求![]() ,并根据图中的数据,用分层抽样的方法抽取
,并根据图中的数据,用分层抽样的方法抽取![]() 个元件,元件寿命落在
个元件,元件寿命落在![]() 之间的应抽取几个?
之间的应抽取几个?
(2)从(1)中抽出的寿命落在![]() 之间的元件中任取
之间的元件中任取![]() 个元件,求事件“恰好有一个元件寿命落在
个元件,求事件“恰好有一个元件寿命落在![]() 之间,一个元件寿命落在
之间,一个元件寿命落在![]() 之间”的概率.
之间”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,一经推出便风靡全国,甚至涌现出一批在微信的朋友圈内销售商品的人(被称为微商).为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:

(1)根据以上数据,能否有60%的把握认为“微信控”与”性别“有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,从这5人中再随机抽取3人赠送200元的护肤品套装,求这3人中“微信控”的人数为2的概率.
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() :
:![]() ,过焦点
,过焦点![]() 斜率大于零的直线
斜率大于零的直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点,且与其准线交于点
两点,且与其准线交于点![]() .
.

(Ⅰ)若线段![]() 的长为
的长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)在![]() 上是否存在点
上是否存在点![]() ,使得对任意直线
,使得对任意直线![]() ,直线
,直线![]() ,
,![]() ,
,![]() 的斜率始终成等差数列,若存在求点
的斜率始终成等差数列,若存在求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,
上,![]() ,过
,过![]() ,
,![]() 的平面
的平面![]() 与此长方体的面相交,交线围成一个正方形.
与此长方体的面相交,交线围成一个正方形.
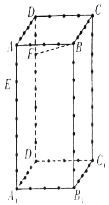
(1)在图中画出这个正方形(不必说明画法和理由);
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(注:图中未标注名称的点均为线段等分点,仅为(1)中作图提供参考.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E、F、G分别为线段PC、PD、BC的中点,现将△PDC折起,使平面PDC⊥平面ABCD(图(2)).

(1)求证:AP∥平面EFG;
(2)若点Q是线段PB的中点,求证:PC⊥平面ADQ;
(3)求三棱锥C-EFG的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com