
【题目】已知函数f(x)=x3﹣3x.
(Ⅰ)求函数f(x)的极值;
(Ⅱ)若关于x的方程f(x)=k有3个实根,求实数k的取值范围.
【答案】解:(I)∵f(x)=x3﹣3x,∴f′(x)=3(x﹣1)(x+1),
令f′(x)=0,解得x=﹣1或x=1,列表如下:
x | (﹣∞,﹣1) | ﹣1 | (﹣1,1) | 1 | (1,+∞) |
f′(x) | + | 0 | ﹣ | 0 | + |
f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
当x=﹣1时,有极大值f(﹣1)=2;
当x=1时,有极小值f(1)=﹣2.
(II)要f(x)=k有3个实根,
由(I)知:f(1)<k<f(﹣1),
即﹣2<k<2,
∴k的取值范围是(﹣2,2)
【解析】(Ⅰ)求出函数的导数,解关于导函数的方程,求出函数的单调区间,从而求出函数的极值即可;(Ⅱ)问题转化为y=f(x)和y=k有3个交点,根据f(x)的极大值和极小值求出k的范围即可.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:高中数学 来源: 题型:
【题目】某县政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
,![]() ,…,
,…,![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
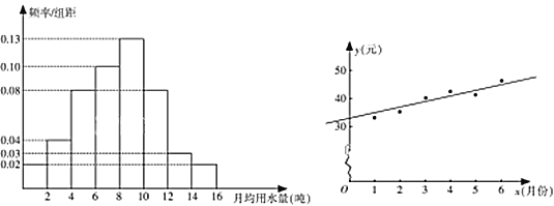
(图1) (图2)
(Ⅰ)通过频率分布直方图,估计该市居民每月的用水量的平均数和中位数(精确到0.01);
(Ⅱ)求用户用水费用![]() (元)关于月用水量
(元)关于月用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(Ⅲ)如图2是该县居民李某2017年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥![]() ,其中
,其中![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值;
的平面角的余弦值;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx.
(1)求f(x)的单调区间和极值;
(2)设A(x1 , f(x1)),B(x2 , f(x2)),且x1≠x2 , 证明: ![]() <f′(
<f′( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣2a|,a∈R.
(1)若不等式f(x)<1的解集为{x|1<x<3},求a的值;
(2)若存在x0∈R,使f(x0)+x0<3,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,已知角A,B,C所对的边分别为a,b,c, ![]() +
+ ![]() =
= ![]() ,b=4,且a>c.
,b=4,且a>c.
(1)求ac的值;
(2)若△ABC的面积为2 ![]() ,求a,c的值.
,求a,c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com