
【题目】设U=R,集合A={x|x2+3x+2=0},B={x|x2+(m+1)x+m=0},若(![]() A)∩B=,求m的值.
A)∩B=,求m的值.
【答案】m=1或2
【解析】方法一:A={-2,-1},
由(![]() A)∩B=得BA,
A)∩B=得BA,
∵方程x2+(m+1)x+m=0的判别式:
Δ=(m+1)2-4m=(m-1)2≥0,∴B≠,
∴B={-1}或B={-2}或B={-1,-2}.
①若B={-1},则m=1;
②若B={-2},则应有-(m+1)=(-2)+(-2)=-4且m=(-2)·(-2)=4,这两式不能同时成立,
∴B≠{-2};
③若B={-1,-2},则应有-(m+1)=(-1)+(-2)=-3且m=(-1)·(-2)=2,由这两式得m=2.
经检验知m=1和m=2符合条件.∴m=1或2.
方法二:本题集合B中的方程的根是x1=-1,x2=-m.
当-m≠-1时集合B={-1,-m},此时只能A=B,即m=2;当-m=-1时集合B={-1},此时集合B是集合A的真子集,也符合要求.∴m=1或2.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明:![]() 为等比数列;
为等比数列;
(3)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过定点P(-2,1)作直线l分别与x、y轴交于A、B两点,
(1)求经过点P且在两坐标轴上的截距相等的直线l方程.
(2)求使![]() 面积为4时的直线l方程。
面积为4时的直线l方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 越大,说明“
越大,说明“![]() 与
与![]() 有关系”的可信度越大.
有关系”的可信度越大.
②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() 的值分别是
的值分别是![]() 和0.3.
和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为![]() 中,
中, ![]() ,
,
则![]() .正确的个数是( )
.正确的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+![]() 有如下性质:如果常数t>0,那么该函数在(0,
有如下性质:如果常数t>0,那么该函数在(0, ![]() ]上是减函数,在[
]上是减函数,在[![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)已知f(x)=![]() ,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=-x-2a,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图像经过坐标原点,其到函数为
的图像经过坐标原点,其到函数为![]() ,数列的前
,数列的前![]() 项和为
项和为![]() ,点
,点![]()
![]() 均在函数
均在函数![]() 的图像上.
的图像上.
(I)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() n项和,求使得
n项和,求使得![]() <
<![]() 对所有都成立的最小正整数m.
对所有都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知椭圆方程为![]() ,点
,点![]() .
.
i.若关于原点对称的两点![]() 记直线
记直线![]() 的斜率分别为
的斜率分别为![]() ,试计算
,试计算![]() 的值;
的值;
ii.若关于原点对称的两点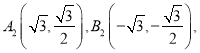 记直线
记直线![]() 的斜率分别为
的斜率分别为![]() ,试计算
,试计算![]() 的值;
的值;
(2)根据上题结论探究:若![]() 是椭圆
是椭圆![]() 上关于原点对称的两点,点
上关于原点对称的两点,点![]() 是椭圆上任意一点,且直线
是椭圆上任意一点,且直线![]() 的斜率都存在,并分别记为
的斜率都存在,并分别记为![]() ,试猜想
,试猜想![]() 的值,并加以证明.
的值,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com