练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】节日前夕，小李在家门前的树上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，且都在通电后的4秒内任一时刻等可能发生，然后每串彩灯以4秒为间隔闪亮，那么这两串彩灯同时通电后，它们第一次闪亮的时候相差不超过2秒的概率是（ ）
    A.
    B.
    C.
    D.

    【答案】C
    【解析】解：设两串彩灯第一次闪亮的时刻分别为x，y，

    由题意可得0≤x≤4，0≤y≤4，

    它们第一次闪亮的时候相差不超过2秒，则|x﹣y|≤2，

    由几何概型可得所求概率为上述两平面区域的面积之比，

    由图可知所求的概率为： =

    故选C

    【考点精析】通过灵活运用几何概型，掌握几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某省高考改革新方案，不分文理科，高考成绩实行“3+3”的构成模式，第一个“3”是语文、数学、外语，每门满分150分，第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试，每门满分100分，高考录取成绩卷面总分满分750分．为了调查学生对物理、化学、生物的选考情况，将“某市某一届学生在物理、化学、生物三个科目中至少选考一科的学生”记作学生群体S，从学生群体S中随机抽取了50名学生进行调查，他们选考物理，化学，生物的科目数及人数统计如表：

    选考物理、化学、生物的科目数

    1

    2

    3

    人数

    5

    25

    20

    （I）从所调查的50名学生中任选2名，求他们选考物理、化学、生物科目数量不相等的概率；
    （II）从所调查的50名学生中任选2名，记X表示这2名学生选考物理、化学、生物的科目数量之差的绝对值，求随机变量X的分布列和数学期望；
    （III）将频率视为概率，现从学生群体S中随机抽取4名学生，记其中恰好选考物理、化学、生物中的两科目的学生数记作Y，求事件“y≥2”的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在两块钢板上打孔，用钉帽呈半球形、钉身为圆柱形的铆钉(图1)穿在一起，在没有帽的一端锤打出一个帽，使得与钉帽的大小相等.铆合的两块钢板，成为某种钢结构的配件，其截面图如图2.(单位：mm，加工中不计损失).

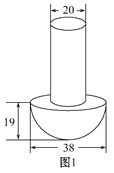
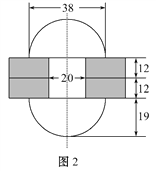
    (1)若钉身高度是钉帽高度的2倍，求铆钉的表面积.

    (2)若每块钢板的厚度为12mm，求钉身的长度(结果精确到1 mm).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设命题p：直线mx﹣y+1=0与圆（x﹣2）2+y2=4有公共点；设命题q：实数m满足方程 + =1表示双曲线．
    （1）若“p∧q”为真命题，求实数m的取值范围；
    （2）若“p∧q”为假命题，“p∨q”为真命题，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=是定义在[-l，1]上的奇函数，且f（）=。

    （1）确定函数f（x）的解析式；

    （2）判断并用定义证明f（x）在（-1，1）上的单调性；

    （3）若f（1-3m）+f（1+m）≥0，求实数m的所有可能的取值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在上的函数，如果满足：对任意，存在常数，都有成立，则称是上的有界函数，其中称为函数的上界，已知函数．

    （Ⅰ）若是奇函数，求的值．

    （Ⅱ）当时，求函数在上的值域，判断函数在上是否为有界函数，并说明理由．

    （Ⅲ）若函数在上是以为上界的函数，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，(其中A＞0，ω＞0，0＜φ＜)的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为M(，－2)．

    （1）求f(x)的解析式；

    （2）将函数f(x)的图象向右平移个单位后，再将所得图象上各点的横坐标缩小到原来的，纵坐标不变，得到y＝g(x)的图象，求函数y＝g(x)的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了预防流感，某学校对教室用药熏消毒法进行消毒.已知药物释放过程中，室内每立方米空气中的含药量（毫克）与时间（小时）成正比；药物释放完毕后，与的函数关系式为（为常数），如图所示.据图中提供的信息，回答下列问题：

    （1）写出从药物释放开始，每立方米空气中的含药量（毫克）与时间（小时）之间的函数关系式；

    （2）据测定，当空气中每立方米的含药量降低到毫克以下时，学生方可进教室。那么药物释放开始，至少需要经过多少小时后，学生才能回到教室？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知幂函数，且在上单调递增.

    （1）求实数的值，并写出相应的函数的解析式；

    （2）若在区间上不单调，求实数的取值范围；

    （3）试判断是否存在正数，使函数在区间上的值域为，若存在，求出的值；若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案