已知挑选空军飞行学员可以说是“万里挑一”,要想通过需过“五关”--目测、初检、复检、文考、政审等.若某校甲、乙、丙三个同学都顺利通过了前两关,有望成为光荣的空军飞行学员.根据分析,甲、乙、丙三个同学能通过复检关的概率分别是0.5,0.6,0.75,能通过文考关的概率分别是0.6,0.5,0.4,通过政审关的概率均为1.后三关相互独立.
(1)求甲、乙、丙三个同学中恰有一人通过复检的概率;
(2)设通过最后三关后,能被录取的人数为X,求随机变量X的期望E(X).
解:甲、乙、丙三位同学分别通过复检为事件A,B,C,则可得P(A)=0.5,P(B)=0.6,P(C)=0.75
(1)甲、乙、丙三位同学中恰好有一人通过复检即为事件
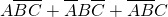
,
利用相互独立事件的概率公式可得P(
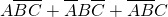
)
=0.5×(1-0.6)×(1-0.7)+(1-0.5)×0.6×(1-0.7)+(1-0.5)×(1-0.6)×0.7=0.275
(2)易知甲、乙、丙每位同学被录取的概率均为0.3,故可看成是独立重复实验,
∴
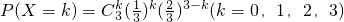
,
P(X=1)=3×(1-0.3)
2×0.3=0.441,
P(X=2)=3×0.3
2×0.7=0.189,
P(X=3)=0.3
3=0.027.
∴E(X)=1×0.441+2×0.189+3×0.027=0.9
分析:(1)设甲、乙、丙三位同学分别通过复检为事件A,B,C,恰好有一人通过复检即为事件
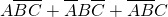
,然后利用相互独立事件的概率公式可得P(
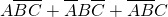
);
(2)易知甲、乙、丙每位同学被录取的概率均为0.3,X的取值可能为0,1,2,3,求出相应的概率,然后利用数学期望公式解之即可.
点评:本题 主要考查了离散型随机变量的期望,同时考查了相互独立事件的概率公式,属于中档题.

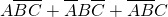 ,
,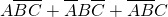 )
)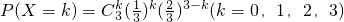 ,
,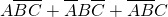 ,然后利用相互独立事件的概率公式可得P(
,然后利用相互独立事件的概率公式可得P( 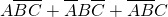 );
);

 阅读快车系列答案
阅读快车系列答案