
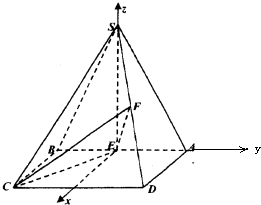
 如图,四棱锥S-ABCD的底面ABCD是正方形,侧面SAB是等腰三角形且垂直于底面,SA=SB=
如图,四棱锥S-ABCD的底面ABCD是正方形,侧面SAB是等腰三角形且垂直于底面,SA=SB=| 5 |
| 1 |
| 2 |
| SB |
| SC |
| n |
|
| n |
| EF |
| 1 |
| 2 |
| EF |
| n |
| m |
| EC |
| EF |
| 1 |
| 2 |
|
| m |
| p |
| m |
| n |
| -2 | ||
|
| 2 |
| 3 |
| 2 |
| 3 |


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
 如图,摩天轮上一点P在t时刻距离地面高度满足y=Asin(ωt+φ)+b,φ∈
如图,摩天轮上一点P在t时刻距离地面高度满足y=Asin(ωt+φ)+b,φ∈查看答案和解析>>
科目:高中数学 来源: 题型:
| A、方程x2-4x+3=0有两个不等的实根 |
| B、解一元一次方程的步骤是去分母、去括号、移项、合并同类项、化系数为1 |
| C、从中山到北京先坐汽车,再坐火车 |
| D、解不等式ax+3>0时,第一步移项,第二步讨论 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com