
【题目】设椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,下顶点为
,下顶点为![]() ,线段
,线段![]() 的中点为
的中点为![]() (
(![]() 为坐标原点),如图,若抛物线
为坐标原点),如图,若抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且经过
,且经过![]() 点.
点.

(1)求椭圆![]() 的方程;
的方程;
(2)设![]() ,
,![]() 为抛物线
为抛物线![]() 上的一动点,过点
上的一动点,过点![]() 作抛物线
作抛物线![]() 的切线交椭圆
的切线交椭圆![]() 于点
于点![]() 、
、![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十一国庆节期间,某商场举行购物抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为![]() ,中奖可以获得3分;方案乙的中奖率为
,中奖可以获得3分;方案乙的中奖率为![]() ,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.
,中奖可以获得2分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,抽奖结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为![]() ,求
,求![]() 的概率;
的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,分别求两种方案下小明、小红累计得分的分布列,并指出为了累计得分较大,两种方案下他们选择何种方案较好,并给出理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)令![]() ,是否存在实数
,是否存在实数![]() ,当
,当![]() (
(![]() 是自然常数)时,函数
是自然常数)时,函数![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)当![]() 时,证明:
时,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线
上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线![]() ,又已知直线
,又已知直线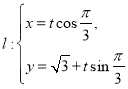 (
(![]() 是参数),且直线
是参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(I)求曲线![]() 的直角坐标方程,并说明它是什么曲线;
的直角坐标方程,并说明它是什么曲线;
(II)设定点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国的高铁技术发展迅速,铁道部门计划在![]() 两城市之间开通高速列车,假设列车在试运行期间,每天在
两城市之间开通高速列车,假设列车在试运行期间,每天在![]() 两个时间段内各发一趟由
两个时间段内各发一趟由![]() 城开往
城开往![]() 城的列车(两车发车情况互不影响),
城的列车(两车发车情况互不影响),![]() 城发车时间及概率如下表所示:
城发车时间及概率如下表所示:
发车 时间 |
|
|
|
|
|
|
概率 |
|
|
|
|
|
|
若甲、乙两位旅客打算从![]() 城到
城到![]() 城,他们到达
城,他们到达![]() 火车站的时间分别是周六的
火车站的时间分别是周六的![]() 和周日的
和周日的![]() (只考虑候车时间,不考虑其他因素).
(只考虑候车时间,不考虑其他因素).
(1)设乙候车所需时间为随机变量![]() (单位:分钟),求
(单位:分钟),求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)求甲、乙两人候车时间相等的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com