练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    直线l过抛物线y2=2px(p＞0)的焦点，且与抛物线相交于A（x1,y1）和B（x2,y2）.

    (1)求证：x1x2=,y1y2=-p2;

    (2)若l的倾斜角为α，求证：|AB|=.

    分析：设出直线方程，利用韦达定理解决.

    证明：（1）若l的斜率存在，设l：y=k(x-)(k≠0)代入y2=2px,消去y整理得k2x2-(k2p+2p)x+=0，由韦达定理得x1x2=.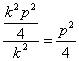

    ∵y12=2px1,y22=2px2,∴y12y22=4p2x1x2=p4,

    ∵y1y2＜0,∴y1y2=-p2.

    若l斜率不存在，x1=x2=,此时x1x2=,y1y2=-p2，结论也成立.

    ∴x1x2=,y1y2=-p2.

    （2）若l斜率存在，由（1）知x1+x2=.

    ∴|AB|=|AF|+|FB|=x1-(-)+x2-(-)=x1+x2+p=

    .

    若l斜率不存在，α=时，|AB|=2p，结论也成立.∴|AB|=.

    点拨：涉及直线与抛物线相交问题在求解时应特别注意直线斜率不存在的情况，要记住过焦点的弦中有x1x2，y1y2为定值，弦长大于或等于2p.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设斜率为2的直线l过抛物线y2=ax（a≠0）的焦点F，且和y轴交于点A，若△OAF（O为坐标原点）的面积为4，则抛物线方程为（　　）
    A、y2=±4xB、y2=4xC、y2=±8xD、y2=8x

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知斜率为2的直线l过抛物线y2=ax的焦点F，且与y轴相交于点A，若△OAF（O为坐标原点）的面积为4，则抛物线方程为（　　）
    A、y2=4xB、y2=8xC、y2=4x或y2=-4xD、y2=8x或y2=-8x

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设斜率为k的直线l过抛物线y2=8x的焦点F，且和y轴交于点A，若△OAF （O为坐标原点）的面积为4，则实数k的值为（　　）
    A、±2B、±4C、2D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系xOy中，直线l过抛物线y2=4x的焦点F交抛物线于A、B两点．
    （1）若|AB|=8，求直线l的斜率
    （2）若|AF|=m，|BF|=n．求证
    1
    m
    +
    1
    n
    为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）直线l过抛物线y2=2px（p＞0）的焦点，且与抛物线相交于A（x1，y1），B（x2，y2）两点，证明：y1y2=-p2；
    （2）直线l过抛物线y2=2px（p＞0）的焦点，且与抛物线相交于A（x1，y1），B（x2，y2）两点，点C在抛物线的准线上，且BC∥x轴，证明：直线AC经过原点．

    查看答案和解析>>

    同步练习册答案