
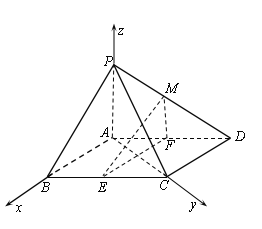
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.

(Ⅰ)求证:EF⊥平面PAC;
(Ⅱ)若M为PD的中点,求证:ME∥平面PAB;
(Ⅲ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求![]() 的值.
的值.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)![]()
【解析】
试题分析:![]() 由平行四边形的性质可得
由平行四边形的性质可得![]() ,即
,即![]() ,由面面垂直的性质得出
,由面面垂直的性质得出![]() 平面
平面![]() ,故
,故![]() ,从而
,从而![]() 平面
平面![]()
![]() 以
以![]() 为原点建立空间直角坐标系,设
为原点建立空间直角坐标系,设![]() ,
,![]() ,求出平面
,求出平面![]() ,平面
,平面![]() 的法向量
的法向量![]() 以及
以及![]() 的坐标,根据线面角相等列方程求解即可得到答案
的坐标,根据线面角相等列方程求解即可得到答案
解析:(1)证明:在平行四边形![]() 中,因为
中,因为![]() ,
,![]() ,
,
所以![]() .由
.由![]() 分别为
分别为![]() 的中点,得
的中点,得![]() , 所以
, 所以![]() .
.
因为侧面![]() 底面
底面![]() ,且
,且![]() ,所以
,所以![]() 底面
底面![]() .
.
又因为![]() 底面
底面![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)解:因为![]() 底面
底面![]() ,
,![]() ,所以
,所以![]() 两两
两两
垂直,以![]() 分别为
分别为![]() 、
、![]() 、
、![]() ,建立空间直角坐标系,则
,建立空间直角坐标系,则
![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,易得平面
,易得平面
![]() 的法向量
的法向量![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() ,
,![]() ,得
,得![]() 令
令![]() , 得
, 得![]() .
.
因为直线![]() 与平面
与平面![]() 所成的角和此直线与平面
所成的角和此直线与平面![]() 所成的角相等,
所成的角相等,
所以![]() ,即
,即![]() ,所以
,所以 ![]() ,
,
解得![]() ,或
,或![]() (舍). 综上所得:
(舍). 综上所得:![]()


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】某社区为了解居民参加体育锻炼的情况,从该社区随机抽取了18名男性居民和12名女性居民,对他们参加体育锻炼的情况进行问卷调查.现按是否参加体育锻炼将居民分成两类:甲类(不参加体育锻炼)、乙类(参加体育锻炼),结果如下表:
甲类 | 乙类 | |
男性居民 | 3 | 15 |
女性居民 | 6 | 6 |
(Ⅰ)根据上表中的统计数据,完成下面的![]() 列联表;
列联表;
男性居民 | 女性居民 | 总计 | |
不参加体育锻炼 | |||
参加体育锻炼 | |||
总计 |
(Ⅱ)通过计算判断是否有90%的把握认为参加体育锻炼与否与性别有关?
附: ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡.若顾客甲没有银联卡,顾客乙只带了现金,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中的三种结账方式,那么他们结账方式的可能情况有( )种
A. 19B. 7C. 26D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项选拔共有四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰,.已知某选手能正确回答第一、二、三、四轮的问题的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(1)求该选手进入第四轮才被淘汰的概率;
(2)求该选手至多进入第三轮考核的概率;
(3)求该选手回答过四个问题的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() ,双曲线
,双曲线![]() 的左、右焦点分别为F1,F2,M是双曲线C2的一条渐近线上的点,且OM⊥MF2,O为坐标原点,若
的左、右焦点分别为F1,F2,M是双曲线C2的一条渐近线上的点,且OM⊥MF2,O为坐标原点,若![]() ,且双曲线C1,C2的离心率相同,则双曲线C2的实轴长是 ( )
,且双曲线C1,C2的离心率相同,则双曲线C2的实轴长是 ( )
A. 32 B. 4 C. 8 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)。在以坐标原点为极点,
为参数)。在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 。
。
(1)写出曲线![]() ,
,![]() 的普通方程;
的普通方程;
(2)过曲线![]() 的左焦点且倾斜角为
的左焦点且倾斜角为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区上年度电价为![]() 元/(
元/(![]() ),年用电量为
),年用电量为![]() .本年度该地政府实行惠民政策,要求电力部门让利给用户,将电价下调到
.本年度该地政府实行惠民政策,要求电力部门让利给用户,将电价下调到![]() 元/(
元/(![]() )至
)至![]() 元/(
元/(![]() )之间,而用户的期望电价为
)之间,而用户的期望电价为![]() 元/(
元/(![]() ).经测算,下调电价后新增用电量和实际电价与用户的期望电价的差成反比(比例系数为
).经测算,下调电价后新增用电量和实际电价与用户的期望电价的差成反比(比例系数为![]() ).该地区的电力成本价为
).该地区的电力成本价为![]() 元/(
元/(![]() ).
).
(1)写出本年度电价下调后电力部门的收益![]() (单位:元)关于实际电价
(单位:元)关于实际电价![]() (单位:元/(
(单位:元/(![]() )的函数解析式;(收益
)的函数解析式;(收益![]() 实际用电量
实际用电量![]() (实际电价
(实际电价![]() 成本价))
成本价))
(2)设![]() ,当电价最低定为多少时,可保证电力部门的收益比上年至多减少
,当电价最低定为多少时,可保证电力部门的收益比上年至多减少![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的的参数方程为
的的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点(
两点(![]() 在
在![]() 轴上方),求
轴上方),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com