
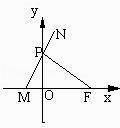
【题目】已知定点F(1,0),动点P(异于原点)在y轴上运动,连接FP,过点P作PM交x轴于点M,并延长MP到点N,且 ![]() ,
, ![]() .
.
(1)求动点N的轨迹C的方程;
(2)若直线l与动点N的轨迹交于A、B两点,若 ![]() 且
且 ![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
【答案】
(1)解:设动点N(x,y),则M(﹣x,0),P(0, ![]() )(x>0),
)(x>0),
∵PM⊥PF,∴kPMkPF=﹣1,即 ![]() ,
,
∴y2=4x(x>0)即为所求
(2)解:设直线l方程为y=kx+b,l与抛物线交于点A(x1,y1)、B(x2,y2),
则由 ![]() ,得x1x2+y1y2=﹣4,即
,得x1x2+y1y2=﹣4,即 ![]() +y1y2=﹣4,∴y1y2=﹣8,
+y1y2=﹣4,∴y1y2=﹣8,
由 ![]() 可得 ky2﹣4y+4b=0(其中k≠0),∴y1y2=
可得 ky2﹣4y+4b=0(其中k≠0),∴y1y2= ![]() =﹣8,b=﹣2k,
=﹣8,b=﹣2k,
当△=16﹣16kb=16(1+2k2)>0时,
|AB|2=(1+ ![]() )
) ![]() =
= ![]() [
[ ![]() ﹣4y1y2]=
﹣4y1y2]= ![]() (
( ![]() +32).
+32).
由题意, ![]() ,
,
可得16×6≤ ![]() (
( ![]() +32)≤16×30,即4≤
+32)≤16×30,即4≤ ![]() ≤28,
≤28,
即 ![]() ,解得
,解得 ![]() ≤k2≤1,
≤k2≤1,
∴ ![]() ≤k≤1,或﹣1≤k≤﹣
≤k≤1,或﹣1≤k≤﹣ ![]() .
.
即所求k的取值范围是[﹣1,﹣ ![]() ]∪[
]∪[ ![]() 1].
1].
【解析】(1)设出动点N,则M,P的坐标可表示出,利用PM⊥PF,kPMspan>kPF=﹣1,求得x和y的关系式,即N的轨迹方程.(2)设出直线l的方程,A,B的坐标,根据 ![]() ,推断出x1x2+y1y2=﹣4进而求得y1y2的值,把直线与抛物线方程联立消去x求得y1y2的表达式,进而气的b和k的关系式,利用弦长公式表示出|AB|2 , 根据|AB|的范围,求得k的范围.
,推断出x1x2+y1y2=﹣4进而求得y1y2的值,把直线与抛物线方程联立消去x求得y1y2的表达式,进而气的b和k的关系式,利用弦长公式表示出|AB|2 , 根据|AB|的范围,求得k的范围.
【考点精析】认真审题,首先需要了解直线的斜率(一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα).


科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,所有棱长均为2,O是底面正方形ABCD中心,E为PC中点,则直线OE与直线PD所成角为( ) 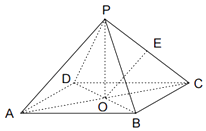
A.30°
B.60°
C.45°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列4个命题,其中正确的命题是 ①“ ![]() ”是“
”是“ ![]() 不共线”的充要条件;
不共线”的充要条件;
②已知向量 ![]() 是空间两个向量,若
是空间两个向量,若 ![]() ,则向量
,则向量 ![]() 的夹角为60°;
的夹角为60°;
③抛物线y=﹣x2上的点到直线4x+3y﹣8=0的距离的最小值是 ![]() ;
;
④与两圆A:(x+5)2+y2=49和圆B:(x﹣5)2+y2=1都外切的圆的圆心P的轨迹方程为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,从椭圆 ![]() 上一点P向x轴作垂线,垂足恰为左焦点F1 , 又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且
上一点P向x轴作垂线,垂足恰为左焦点F1 , 又点A是椭圆与x轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且 ![]() . (Ⅰ) 求椭圆的方程;
. (Ⅰ) 求椭圆的方程;
(Ⅱ) 若M是椭圆上的动点,点N(4,2),求线段MN中点Q的轨迹方程.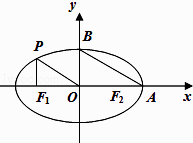
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA的中点. 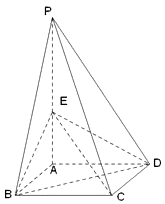
(1)求证:PC∥平面BDE
(2)求三棱锥P﹣CED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列{an}的前n项和为Sn , 已知a1=2,且4S1 , 3S2 , 2S3成等差数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=|2n﹣5|an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() ,左焦点
,左焦点 ![]() ,且离心率
,且离心率 ![]() (Ⅰ)求椭圆C的方程;
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=kx+m(k≠0)与椭圆C交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆C的右顶点A.求证:直线l过定点,并求出定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com