
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,f(x)=2sin(x-A)cosx+sin(B+C)(x∈R),函数f(x)的图象关于点![]() 对称.
对称.
(1)当![]() 时,求f(x)的值域;
时,求f(x)的值域;
(2)若a=7且![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】(1)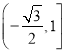 ;(2)
;(2)![]()
【解析】试题分析:
试题解析:(1)∵f(x)=2sin(x-A)cosx+sin(B+C),
∴f(x)=2(sin xcosA-cosxsinA)cosx+sin A
=2sinxcosxcosA-2cos2xsin A+sin A
=sin 2xcos A-cos 2xsin A=sin(2x-A).
∵函数f(x)的图象关于点![]() 对称,∴
对称,∴![]() ,即
,即![]() .
.
又A∈(0,π),∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() 2,∴
2,∴![]() ,
,
即函数f(x)的值域为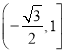
(2)由正弦定理,得![]() ,
,
又∵a=7, ![]() ,∴
,∴![]() .
.
∵![]() ,∴b+c=13.
,∴b+c=13.
由余弦定理,得49=b2+c2-bc,即49=(b+c)2-3bc=169-3bc,
∴bc=40,∴ ![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,设倾斜角为
中,设倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数)与曲线
为参数)与曲线 (
(![]() 为参数)相交于不同的两点
为参数)相交于不同的两点![]() 、
、![]() .
.
(1)若![]() ,求线段
,求线段![]() 的中点的直角坐标;
的中点的直角坐标;
(2)若直线![]() 的斜率为
的斜率为![]() ,且过已知点
,且过已知点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应我市“创建宜居港城,建设美丽莆田”,某环保部门开展以“关爱木兰溪,保护母亲河”为主题的环保宣传活动,将木兰溪流经市区河段分成![]() 段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如下表:
段,并组织青年干部职工对每一段的南、北两岸进行环保综合测评,得到分值数据如下表:
南岸 | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
北岸 | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
(Ⅰ)记评分在![]() 以上(包括
以上(包括![]() )为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
)为优良,从中任取一段,求在同一段中两岸环保评分均为优良的概率;
(Ⅱ)根据表中数据完成下面茎叶图;
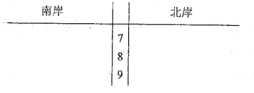
(Ⅲ)分别估计两岸分值的中位数,并计算它们的平均值,试从计算结果分析两岸环保情况,哪边保护更好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() , 直线
, 直线![]() 过点
过点![]() .
.
(Ⅰ)若点![]() 到直线
到直线![]() 的距离为
的距离为![]() , 求直线
, 求直线![]() 的斜率;
的斜率;
(Ⅱ)设![]() 为抛物线上两点, 且
为抛物线上两点, 且![]() 不与
不与![]() 轴垂直, 若线段
轴垂直, 若线段![]() 的垂直平分线恰过点
的垂直平分线恰过点![]() , 求证: 线段
, 求证: 线段![]() 中点的横坐标为定值.
中点的横坐标为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆G: ![]() 的离心率为
的离心率为![]() ,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).
,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).
(Ⅰ)求椭圆G的方程;
(Ⅱ)已知A为椭圆G的左顶点,平行于AM的直线l与椭圆G相交于B,C两点,请判断直线MB,MC是否关于直线m对称,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直角坐标平面内两点P,Q满足条件:①P,Q都在函数y=f(x)的图象上;②P,Q关于原点对称,则称(P,Q)是函数y=f(x)的一个“伙伴点组”(点组(P,Q)与(Q,P)看作同一个“伙伴点组”).已知函数f(x)=![]() 有两个“伙伴点组”,则实数k的取值范围是( )
有两个“伙伴点组”,则实数k的取值范围是( )
A. (-∞,0) B. (0,1)
C. ![]() D. (0,+∞)
D. (0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某销售公司为了解员工的月工资水平,从1000位员工中随机抽取100位员工进行调查,得到如下的频率分布直方图:
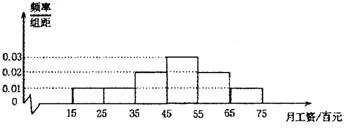
(1)试由此图估计该公司员工的月平均工资;
(2)该公司工资发放是以员工的营销水平为重要依据来确定的,一般认为,工资低于4500。元的员工属于学徒阶段,没有营销经验,若进行营销将会失败;高于4500元的员工是具备营销成熟员工,基进行营销将会成功。现将该样本按照“学徒阶段工资”、“成熟员工工资”分成两层,进行分层抽样,从中抽出5人,在这5人中任选2人进行营销活动。活动中,每位员工若营销成功,将为公司赢得3万元,否则公司将损失1万元。试问在此次比赛中公司收入多少万元的可能性最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com