
【题目】圆x2+y2﹣2x﹣8y+13=0的圆心到直线ax+y﹣1=0的距离为1,则a=( )
A.﹣ ![]()
B.﹣ ![]()
C.![]()
D.2
【答案】A
【解析】解:圆x2+y2﹣2x﹣8y+13=0的圆心坐标为:(1,4),
故圆心到直线ax+y﹣1=0的距离d= ![]() =1,
=1,
解得:a= ![]() ,
,
故选:A.
【考点精析】认真审题,首先需要了解点到直线的距离公式(点![]() 到直线
到直线![]() 的距离为:
的距离为: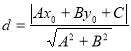 ),还要掌握圆的一般方程(圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显)的相关知识才是答题的关键.
),还要掌握圆的一般方程(圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知复数z1=m+ni(m,n∈R),z=x+yi(x,y∈R),z2=2+4i且 ![]() .
.
(1)若复数z1对应的点M(m,n)在曲线 ![]() 上运动,求复数z所对应的点P(x,y)的轨迹方程;
上运动,求复数z所对应的点P(x,y)的轨迹方程;
(2)将(1)中的轨迹上每一点按向量 ![]() 方向平移
方向平移 ![]() 个单位,得到新的轨迹C,求C的轨迹方程;
个单位,得到新的轨迹C,求C的轨迹方程;
(3)过轨迹C上任意一点A(异于顶点)作其切线,交y轴于点B,求证:以线段AB为直径的圆恒过一定点,并求出此定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是等腰梯形,AD∥BC,BC=2AD,O为BD的中点. 
(1)求证:CD∥平面POA;
(2)若PO⊥底面ABCD,CD⊥PB,AD=PO=2,求二面角A﹣PD﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职业学校的王亮同学到一家贸易公司实习,恰逢该公司要通过海运出口一批货物,王亮同学随公司负责人到保险公司洽谈货物运输期间的投保事宜,保险公司提供了缴纳保险费的两种方案:
①一次性缴纳50万元,可享受9折优惠;
②按照航行天数交纳:第一天缴纳0.5元,从第二天起每天交纳的金额都是其前一天的2倍,共需交纳20天.
请通过计算,帮助王亮同学判断那种方案交纳的保费较低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆A:(x+1)2+y2=16,圆C过点B(1,0)且与圆A相切,设圆心C的轨迹为曲线E.
(Ⅰ)求曲线E的方程;
(Ⅱ)过点B作两条互相垂直的直线l1,l2,直线l1与E交于M,N两点,直线l2与圆A交于P,Q两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,x轴的非负半轴为极轴,并在两坐标系中取相同的长度单位,若直线l的极坐标方程是ρsin(θ+ ![]() )=2
)=2 ![]() ,且点P是曲线C:
,且点P是曲线C: ![]() (θ为参数)上的一个动点.
(θ为参数)上的一个动点.
(Ⅰ)将直线l的方程化为直角坐标方程;
(Ⅱ)求点P到直线l的距离的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC= ![]() ,点E在AD上,且AE=2ED.
,点E在AD上,且AE=2ED. 
(Ⅰ)已知点F在BC上,且CF=2FB,求证:平面PEF⊥平面PAC;
(Ⅱ)当二面角A﹣PB﹣E的余弦值为多少时,直线PC与平面PAB所成的角为45°?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com