
| 5(a1+a5) |
| 2 |
| a | 3 3 |
| a | 2 3 |
| 5(a1+a5) |
| 2 |
| a | 3 3 |
| a | 2 3 |
| 2(2n-1) |
| 2-1 |


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
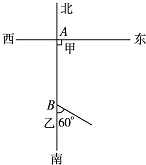 如图,A,B 两个小岛相距21海里,B 岛在 A 岛的正南方,现在甲船从 A 岛出发,以9海里/时的速度向 B 岛行驶,而乙船同时以6海里/时的速度离开 B 岛向南偏东60°方向行驶,行驶多少时间后,两船相距最近?并求出两船的最近距离.
如图,A,B 两个小岛相距21海里,B 岛在 A 岛的正南方,现在甲船从 A 岛出发,以9海里/时的速度向 B 岛行驶,而乙船同时以6海里/时的速度离开 B 岛向南偏东60°方向行驶,行驶多少时间后,两船相距最近?并求出两船的最近距离.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 单价(元) | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 销量(桶) | 480 | 420 | 360 | 300 | 240 | 180 | 120 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com