
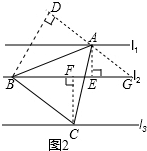
 如图,l1,l2,l3是同一平面内的三条平行直线,l1与l2间的距离是1,l3与l2间的距离是2,正△ABC的三顶点分别在l1,l2,l3上,则△ABC的边长是
如图,l1,l2,l3是同一平面内的三条平行直线,l1与l2间的距离是1,l3与l2间的距离是2,正△ABC的三顶点分别在l1,l2,l3上,则△ABC的边长是2
| ||
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
| BD2+AD2 |
2
| ||
| 3 |
2
| ||
| 3 |


科目:高中数学 来源: 题型:
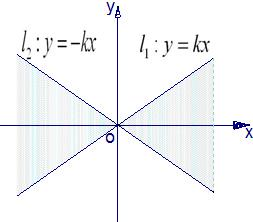 如图,直线l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
如图,直线l1:y=kx(k>0)与直线l2:y=-kx之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.查看答案和解析>>
科目:高中数学 来源: 题型:
 已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).
已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).查看答案和解析>>
科目:高中数学 来源:高考总复习全解 数学 一轮复习·必修课程 (人教实验版) B版 人教实验版 B版 题型:047
如图,l1∥l2,l∩l1=A,l∩l2=B,求证:直线l、l1、l2共面.

查看答案和解析>>
科目:高中数学 来源:高考总复习全解 数学 一轮复习·必修课程 (人教实验版) B版 人教实验版 B版 题型:047
如果三条平行线都与一条直线相交,那么这四条直线共面.
分析:可先由已知条件分别确定平面,然后再证它们是重合的.此题可用归一法证明.
已知:如图,l1∥l2∥l3,l∩l1=A,l∩l2=B,l∩l3=C.

求证:l1、l2、l3、l四条直线共面.
查看答案和解析>>
科目:高中数学 来源:2013年普通高等学校招生全国统一考试江西卷理数 题型:013
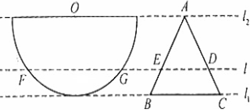
如图,半径为1的半圆O与等边三角形ABC夹在两平行线,l1,l2之间l∥l1,l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点,设弧![]() 的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2,则函数y=f(x)的图像大致是
的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2,则函数y=f(x)的图像大致是
A.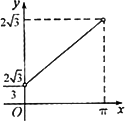
B.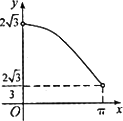
C.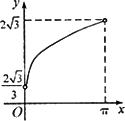
D.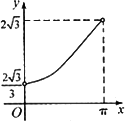
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com