
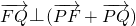 .设动点P的轨迹为曲线C.
.设动点P的轨迹为曲线C.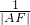 +
+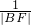 =
= ;
; 与
与 的夹角为θ(O为坐标原点,A、B为(2)中的两点),求cosθ的取值范围.
的夹角为θ(O为坐标原点,A、B为(2)中的两点),求cosθ的取值范围.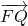 =(-4,y),
=(-4,y), =(2-x,-y),
=(2-x,-y), =(-2-x,0).(3分)
=(-2-x,0).(3分)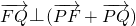 ,得
,得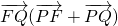 =0,即(-4,y)•(-2x,-y)=0
=0,即(-4,y)•(-2x,-y)=0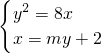 的实数解.
的实数解.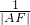 +
+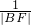 =
=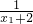 +
+ =
=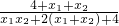 =
= ,得证. (12分)
,得证. (12分) =(x1,y1),
=(x1,y1), =(x2,y2).
=(x2,y2).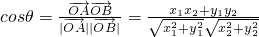 =
=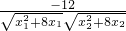 =
=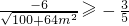 (当且仅当m=0时,等号成立). (16分)
(当且仅当m=0时,等号成立). (16分) ,0). (18分)
,0). (18分)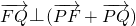 ,得
,得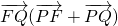 =0,由此可求曲线C的方程;
=0,由此可求曲线C的方程;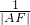 +
+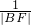 =
=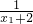 +
+ ,即可证得结论;
,即可证得结论; =(x1,y1),
=(x1,y1), =(x2,y2),利用
=(x2,y2),利用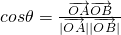 ,可求cosθ的取值范围.
,可求cosθ的取值范围.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 9 |
| 2 |
| 3 |
| 2 |
| PF |
| PF′ |
查看答案和解析>>
科目:高中数学 来源: 题型:
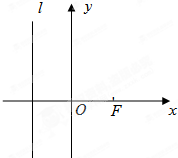 已知定点F(2,0),动圆P经过点F且与直线x=-2相切,记动圆的圆心P的轨迹为C.
已知定点F(2,0),动圆P经过点F且与直线x=-2相切,记动圆的圆心P的轨迹为C.| OM |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| FQ |
| PF |
| PQ |
| 1 |
| |AF| |
| 1 |
| |BF| |
| 1 |
| 2 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| FQ |
| PF |
| PQ |
| 1 |
| |AF| |
| 1 |
| |BF| |
| 1 |
| 2 |
| OA |
| OB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com