
【题目】已知函数f(x)=alnx+(x﹣c)|x﹣c|,a<0,c>0 (Ⅰ)当 ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(Ⅱ)设函数f(x)的图象在点P(x1 , f(x1)),Q(x2 , f(x2))两处的切线分别为l1 , l2 . 若 ![]() ,且l1⊥l2 , 求实数c的最小值.
,且l1⊥l2 , 求实数c的最小值.
【答案】解:函数 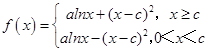 ,求导数
,求导数 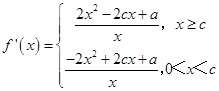 ,
,
(Ⅰ)当 ![]() 时,
时, 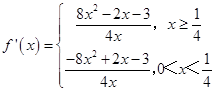 ,
,
若 ![]() ,则
,则 ![]() 恒成立,
恒成立,
所以f(x)在 ![]() 上单调递减;若
上单调递减;若 ![]() ,则
,则 ![]() ,
,
令f'(x)=0,解得 ![]() 或
或 ![]() (舍),
(舍),
当 ![]() 时,f'(x)<0,f(x)在
时,f'(x)<0,f(x)在 ![]() 上单调递减;
上单调递减;
当 ![]() 时,f'(x)>0,f(x)在
时,f'(x)>0,f(x)在 ![]() 上单调递增.
上单调递增.
所以函数f(x)的单调递减区间是 ![]() ,单调递增区间是
,单调递增区间是 ![]()
(Ⅱ)由l1⊥l2知, 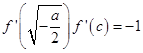 ,而
,而 ![]() ,则
,则 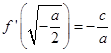 ,
,
若 ![]() ,则
,则 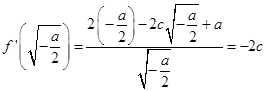
所以 ![]() ,解得
,解得 ![]() ,不符合题意
,不符合题意
故 ![]() ,则
,则 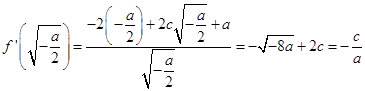
整理得 ![]() ,由c>0,a<0得
,由c>0,a<0得 ![]()
令 ![]() ,则
,则 ![]() ,所以
,所以 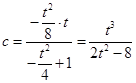
设 ![]() ,当
,当 ![]() 时,g'(t)<0,g(t)在
时,g'(t)<0,g(t)在 ![]() 上单调递减;
上单调递减;
当 ![]() 时,g'(t)>0,g(t)在
时,g'(t)>0,g(t)在 ![]() 上单调递增
上单调递增
所以函数g(t)的最小值为 ![]() ,故实数c的最小值为
,故实数c的最小值为 ![]()
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(Ⅱ)根据垂直关系求出a的范围,令 ![]() ,则
,则 ![]() ,表示出c,根据函数的单调性求出c的最小值即可.
,表示出c,根据函数的单调性求出c的最小值即可.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】f(x)=Acos(ωx+φ)(A,ω>0)的图象如图所示,为得到g(x)=﹣Asin(ωx+ ![]() )的图象,可以将f(x)的图象( )
)的图象,可以将f(x)的图象( ) 
A.向右平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一边长为6的正方形铁片,在铁片的四角各截去一个边长为x的小正方形后,沿图中虚线部分折起,做成一个无盖方盒. 
(1)试用x表示方盒的容积V(x),并写出x的范围;
(2)求方盒容积V(x)的最大值及相应x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}的前四项和S4=14,且a1 , a3 , a7成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Tn为数列{ ![]() }的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
}的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】知f(x)是定义在R上的奇函数,且当x∈(0,+∞)时,f(x)=2018x+log2018x,则函数f(x)的零点个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC-A′B′C′,底面是边长为1的正三角形,侧面为全等的矩形且高为8,求一点自A点出发沿着三棱柱的侧面绕行一周后到达A′点的最短路线长.

本题条件不变,求一点自A点出发沿着三棱柱的侧面绕行两周后到达A′点的最短路线长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体ABCD-A1B1C1D1中,AB=BC=2,D1D=3,点M是B1C1的中点,点N是AB的中点.建立如图所示的空间直角坐标系.
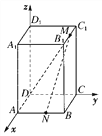
(1)写出点D、N、M的坐标;
(2)求线段MD、MN的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P-ABCD的底面ABCD是正方形,E,F分别为AC和PB上的点,它的直观图,正视图,侧视图如图所示.
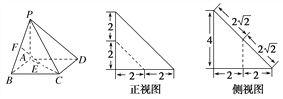
(1)求EF与平面ABCD所成角的大小;
(2)求二面角B-PA-C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com