
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 的焦点为
的焦点为![]() .
.
(1)若过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 有且只有一个交点,求直线
有且只有一个交点,求直线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求
两点,求![]() 的面积.
的面积.
【答案】(1)x=0或y=1或y=x+1;(2) ![]() .
.
【解析】试题分析:
(1)求出![]() ,分类讨论,直线与抛物线方程联立,即可求解直线
,分类讨论,直线与抛物线方程联立,即可求解直线![]() 的方程;
的方程;
(2)直线![]() 与抛物线联立,利用韦达定理,根据
与抛物线联立,利用韦达定理,根据![]() 的面积
的面积![]() ,即可求解
,即可求解![]() 的面积.
的面积.
试题解析:
(1)∵抛物线C:y2=2px(p>0)的焦点为F(1,0),抛物线E:x2=2py的焦点为M,
∴p=2,M(0,1)
斜率不存在时,x=0,满足题意;
斜率存在时,设方程为y=kx+1,代入y2=4x,可得k2x2+(2k﹣4)x+1=0,
k=0时,x=![]() ,满足题意,方程为y=1;
,满足题意,方程为y=1;
k≠0时,△=(2k﹣4)2﹣4k2=0,∴k=1,方程为y=x+1,
综上,直线l的方程为x=0或y=1或y=x+1;
(2)直线MF的方程为y=﹣x+1,代入y2=4x,可得y2+4y﹣4=0,
设A(x1,y1),B(x2,y2),则y1+y2=﹣4,y1y2=﹣4,
∴△OAB的面积S=![]() |OF||y1﹣y2|=
|OF||y1﹣y2|=![]() =2
=2![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过点M的直线与抛物线交于A,B两点,设A(x1 , y1)到准线l的距离d=2λp(λ>0) 
(1)若y1=d=3,求抛物线的标准方程;
(2)若 ![]() +λ
+λ ![]() =
= ![]() ,求证:直线AB的斜率的平方为定值.
,求证:直线AB的斜率的平方为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 为正方形,四边形
为正方形,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若过直线![]() 的一个平面与线段
的一个平面与线段![]() 和
和![]() 分别相交于点
分别相交于点![]() 和
和![]() (点
(点![]() 与点
与点![]() 均不重合),求证:
均不重合),求证: ![]() ;
;
(3)判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱台ABC﹣FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为CE中点, ![]() .
. 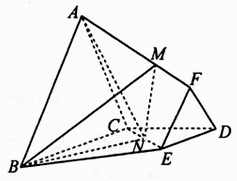
(Ⅰ)λ为何值时,MN∥平面ABC?
(Ⅱ)在(Ⅰ)的条件下,求直线AN与平面BMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=e2x+ln(x+a).
(1)当a=1时,①求f(x)在(0,1)处的切线方程;②当x≥0时,求证:f(x)≥(x+1)2+x.
(2)若存在x0∈[0,+∞),使得 ![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线的
,求直线的![]() 斜率.
斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司进行仓储机器人升级换代期间,第一年有机器人![]() 台,平均每台机器人创收利润
台,平均每台机器人创收利润![]() 万元.预测以后每年平均每台机器人创收利润都比上一年增加
万元.预测以后每年平均每台机器人创收利润都比上一年增加![]() 万元,但该物流公司在用机器人数量每年都比上一年减少
万元,但该物流公司在用机器人数量每年都比上一年减少![]() .
.
(1)设第![]() 年平均每台机器人创收利润为
年平均每台机器人创收利润为![]() 万元,在用机器人数量为
万元,在用机器人数量为![]() 台,求
台,求![]() ,
,![]() 的表达式;
的表达式;
(2)依上述预测,第几年该物流公司在用机器人创收的利润最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com