

 解:如下图所示:试验的全部结果所构成的区域为{(a,b)|0≤a≤1,0≤b≤1}(图中矩形所示).其面积为1.
解:如下图所示:试验的全部结果所构成的区域为{(a,b)|0≤a≤1,0≤b≤1}(图中矩形所示).其面积为1. .
. .
.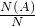 求解.
求解. 

科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:江西省新余一中2012届高三第六次模拟数学理科试题 题型:022
从平面区域G={(a,b)|0≤a≤1,0≤b≤1}内随机取一点(a,b),则使得关于x的方程x2+2bx+a2=0有实根的概率是________.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西南昌10所省高三第二次模拟突破冲刺文科数学(一)(解析版) 题型:填空题
从平面区域G={(a,b)|0≤a≤1,0≤b≤1}内随机取一点(a,b),则使得关于x的方程x2+2bx+a2=0有实根的概率是 _________ .
查看答案和解析>>
科目:高中数学 来源:2012年江西省九江市高考数学一模试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012年江西省九江市高考数学一模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com