|
答:其高为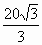 cm时,体积最大. cm时,体积最大.
解:设圆锥底面半径为R,圆锥高为h,
∴h2+R2=202.∴R=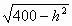 . .
∴圆锥体积V=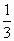 πR2·h= πR2·h=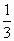 π(400-h2)·h= π(400-h2)·h=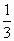 π(400h-h3). π(400h-h3).
令 = =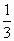 π(400-3h2)=0,∵h>0, π(400-3h2)=0,∵h>0,
∴解得h= . .
当h<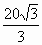 时, 时, >0;当h> >0;当h>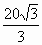 时, 时, <0. <0.
∴当h=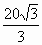 时,V有最大值. 时,V有最大值.
思路解析:解这类有关函数最大值、最小值的实际问题时,首先要把各个变量用字母表示出来,然后需要分析问题中各个变量之间的关系,找出适当的函数关系式,并确定函数的定义区间;接着运用数学知识求解,所得结果要符合问题的实际意义.也就是说最后要进行检验.
| 