
【题目】若对任意的x∈D,均有g(x)≤f(x)≤h(x)成立,则称函数f(x)为函数g(x)到函数h(x)在区间D上的“任性函数”.已知函数f(x)=kx,g(x)=x2﹣2x,h(x)=(x+1)(lnx+1),且f(x)是g(x)到h(x)在区间[1,e]上的“任性函数”,则实数k的取值范围是 .
【答案】[e﹣2,2]
【解析】解:若f(x)是g(x)到h(x)在区间[1,e]上的“任性函数”,
则x∈[1,e]时, ![]() 恒成立,
恒成立,
即 ![]() 恒成立,
恒成立,
即 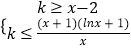 恒成立,
恒成立,
若k≥x﹣2在区间[1,e]上恒成立,则k≥e﹣2;
令 ![]() ,若
,若 ![]() 在区间[1,e]上恒成立,则k≤v(x)min,
在区间[1,e]上恒成立,则k≤v(x)min,
![]() ,
,
令u(x)=x﹣lnx,则u′(x)=1﹣ ![]() ,
,
当x∈[1,e]时,u′(x)≥0恒成立,
则u(x)=x﹣lnx在[1,e]上为增函数,u(x)≥u(1)=1恒成立,
即 ![]() ≥0恒成立,
≥0恒成立,
故 ![]() 在[1,e]上为增函数,
在[1,e]上为增函数,
v(x)≥v(1)=2恒成立,
故k≤2,
综上可得:k∈[e﹣2,2],
所以答案是:[e﹣2,2]
【考点精析】关于本题考查的函数的最大(小)值与导数,需要了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象与函数h(x)=x+ ![]() +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求f(x)的解析式;
(2)若g(x)=f(x)x+ax,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,AB=4 ![]() ,AD=2
,AD=2 ![]() ,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.
,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.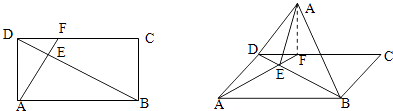
(1)当θ=90°时,求A′C的长;
(2)当cosθ= ![]() 时,求BC与平面A′BD所成角的正弦值.
时,求BC与平面A′BD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 经过点
经过点 ![]() ,左右焦点分别为F1、F2 , 圆x2+y2=2与直线x+y+b=0相交所得弦长为2.
,左右焦点分别为F1、F2 , 圆x2+y2=2与直线x+y+b=0相交所得弦长为2.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设Q是椭圆C上不在x轴上的一个动点,O为坐标原点,过点F2作OQ的平行线交椭圆C于M、N两个不同的点
⑴试探究 ![]() 的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.
的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.
⑵记△QF2M的面积为S1 , △OF2N的面积为S2 , 令S=S1+S2 , 求S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos2x+2 ![]() sinxcosx+a,且当x∈[0,
sinxcosx+a,且当x∈[0, ![]() ]时,f(x)的最小值为2.
]时,f(x)的最小值为2.
(Ⅰ)求a 的值;
(Ⅱ)先将函数y=f (x) 的图象上点的纵坐标不变,横坐标缩小为原来的 ![]() ,再将所得的图象向右平移
,再将所得的图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,求方程g(x)=4在区间[0,
个单位,得到函数y=g(x)的图象,求方程g(x)=4在区间[0, ![]() ]上所有根之和.
]上所有根之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com