
【题目】如图所示的几何体中,正方形![]() 所在平面垂直于平面
所在平面垂直于平面![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,![]() 为
为![]() 上一点,且
上一点,且![]() 平面
平面![]() ,
,![]() .
.
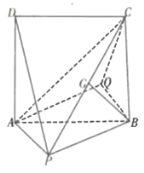
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求直线
体积最大时,求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的各项都是正数,其前
的各项都是正数,其前![]() 项和为
项和为![]() ,且满足:
,且满足:![]() ,
,![]() ,其中
,其中![]() ,常数
,常数![]()
![]() .
.
(1)求证:![]() 是一个定值;
是一个定值;
(2)若数列![]() 是一个周期数列(存在正整数
是一个周期数列(存在正整数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 为周期数列,
为周期数列,![]() 为它的一个周期),求该数列的最小周期;
为它的一个周期),求该数列的最小周期;
(3)若数列![]() 是各项均为有理数的等差数列,
是各项均为有理数的等差数列,![]() (
(![]() ),问:数列
),问:数列![]() 中的所有项是否都是数列
中的所有项是否都是数列![]() 中的项?若是,请说明理由;若不是,请举出反例.
中的项?若是,请说明理由;若不是,请举出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为给定的不小于
为给定的不小于![]() 的正整数,考察
的正整数,考察![]() 个不同的正整数
个不同的正整数![]() ,
,![]() ,
,![]() ,
,![]() 构成的集合
构成的集合![]() ,若集合
,若集合![]() 的任何两个不同的非空子集所含元素的总和均不相等,则称集合
的任何两个不同的非空子集所含元素的总和均不相等,则称集合![]() 为“差异集合”.
为“差异集合”.
(1)分别判断集合![]() ,集合
,集合![]() 是否是“差异集合”;(只需写出结论)
是否是“差异集合”;(只需写出结论)
(2)设集合![]() 是“差异集合”,记
是“差异集合”,记![]() ,求证:数列
,求证:数列![]() 的前
的前![]() 项和
项和![]()
![]() ;
;
(3)设集合![]() 是“差异集合”,求
是“差异集合”,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:
站的地铁票价如下表:
乘坐站数 |
|
|
|
票价(元) |
|
|
|
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站.甲、乙乘坐不超过
站.甲、乙乘坐不超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() ;甲、乙乘坐超过
;甲、乙乘坐超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() .
.
(1)求甲、乙两人付费相同的概率;
(2)设甲、乙两人所付费用之和为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老年人120人,中年人360人,青年人n人,为调查身体健康状况,需要从中抽取一个容量为m的样本,用分层抽样的方法进行抽样调查,样本中的中年人为6人,则n和m的值不可以是下列四个选项中的哪组( )
A.n=360,m=14B.n=420,m=15C.n=540,m=18D.n=660,m=19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第28届金鸡百花电影节将于11月19日至23日在福建省厦门市举办,近日首批影展片单揭晓,《南方车站的聚会》《春江水暖》《第一次的离别》《春潮》《抵达之谜》五部优秀作品将在电影节进行展映.若从这五部作品中随机选择两部放在展映的前两位,则《春潮》与《抵达之谜》至少有一部被选中的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三个顶点
的三个顶点![]() 均在抛物线
均在抛物线![]() 上,给出下列命题:
上,给出下列命题:
①若直线![]() 过点
过点![]() ,则存在
,则存在![]() 使抛物线
使抛物线![]() 的焦点恰为
的焦点恰为![]() 的重心;
的重心;
②若直线![]() 过点
过点![]() ,则存在点
,则存在点![]() 使
使![]() 为直角三角形;
为直角三角形;
③存在![]() ,使抛物线
,使抛物线![]() 的焦点恰为
的焦点恰为![]() 的外心;
的外心;
④若边![]() 的中线
的中线![]() 轴,
轴,![]() ,则
,则![]() 的面积为
的面积为![]() .
.
其中正确的序号为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com