
【题目】正四面体ABCD中,M是棱AD的中点,O是点A在底面BCD内的射影,则异面直线BM与AO所成角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:取BC中点E,DC中点F,连结DE、BF,则由题意得DE∩BF=O,
取OD中点N,连结MN,则MN∥AO,

∴∠BMN是异面直线BM与AO所成角(或所成角的补角),
设正四面体ABCD的棱长为2,由BM=DE= ![]() ,OD=
,OD= ![]() ,
,
∴AO= ![]() =
= ![]() ,∴MN=
,∴MN= ![]() ,
,
∵O是点A在底面BCD内的射影,MN∥AO,∴MN⊥平面BCD,
∴cos∠BMN= ![]() =
= ![]() =
= ![]() ,
,
∴异面直线BM与AO所成角的余弦值为 ![]() .
.
故选:B.
【考点精析】利用异面直线及其所成的角对题目进行判断即可得到答案,需要熟知异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.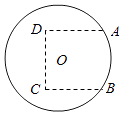
(1)若正方形边长为10米,求广场的面积;
(2)求铺设的4条线路OA,OB,OC,OD总长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年5月17日为国际电信日,某市电信公司每年在电信日当天对办理应用套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元.根据以往的统计结果绘出电信日当天参与活动的统计图,现将频率视为概率.
(1)求某两人选择同一套餐的概率;
(2)若用随机变量X表示某两人所获优惠金额的总和,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点P是双曲线 ![]() 的右支上一点,其左,右焦点分别为F1 , F2 , 直线PF1与以原点O为圆心,a为半径的圆相切于A点,线段PF1的垂直平分线恰好过点F2 , 则离心率的值为( )
的右支上一点,其左,右焦点分别为F1 , F2 , 直线PF1与以原点O为圆心,a为半径的圆相切于A点,线段PF1的垂直平分线恰好过点F2 , 则离心率的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(2,3)在椭圆 ![]() 上,设A,B,C分别为椭圆的左顶点、上顶点、下顶点,且点C到直线AB的距离为
上,设A,B,C分别为椭圆的左顶点、上顶点、下顶点,且点C到直线AB的距离为 ![]() .
.
(I)求椭圆C的方程;
(II)设M(x1 , y1),N(x2 , y2)(x1≠x2)为椭圆上的两点,且满足 ![]()
![]() =
= ![]() ,求证:△MON的面积为定值,并求出这个定值.
,求证:△MON的面积为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣a+lnx.
(Ⅰ)若a=1,求证:当x>1时,f(x)>2x﹣1;
(Ⅱ)若存在x0≥e,使f(x0)<2lnx0 , 求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中有大小相同,编号分别为1,2,3,4,5的五个球,从中有放回地每次取一个球,共取3次,取得三个球的编号之和不小于13的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F(1,0),直线l:x=﹣1,直线l'垂直l于点P,线段PF的垂直平分线交l'于点Q.
(1)求点Q的轨迹方程C;
(2)过F做斜率为 ![]() 的直线交C于A,B,过B作l平行线交C于D,求△ABD外接圆的方程.
的直线交C于A,B,过B作l平行线交C于D,求△ABD外接圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com