分析:(1)先根据条件得到四边形BFD1E是棱形,设H是EF中点,再结合条件得到EF⊥面GHD1,⇒平面BFD1E⊥平面GHD1,然后作GK⊥HD1,在RT△GHD1中求出GK的长即可得到结论;
(2)先根据A1C1∥EF⇒A1C1∥平面BFD1E,进而得到G到平面BFD1E的距离就是四棱锥A1-BFD1E的高,再代入体积计算公式即可得到答案.
解答:解:(1)由题得:
BE=BF=FD1=ED1=a,
∴四边形BFD
1E是棱形,连接EF和BD
1,
有A
1C
1∥EF,设H是EF中点,
连GH、GD
1,则EF⊥GH,EF⊥HD
1,
∴EF⊥面GHD
1,又EF?面BFD
1E中,
∴平面BFD
1E⊥平面GHD
1,
作GK⊥HD
1,则GK⊥面BFD
1E,
则G到平面的距离就是KG长.在RT△GHD
1中,
GH•GD
1=
GK•HD
1.
又
GH=a,
GD1=a,
HD1=a,
∴
GK=a.
(2)∵A
1C
1∥EF,∴A
1C
1∥平面BFD
1E,
∴G到平面BFD
1E的距离就是四棱锥A
1-BFD
1E的高,
∴
VA1-BFD1E=S菱形BFD1E•GK=•EF•BD1•GK=•a•a•a=a3 点评:本题主要考查点到面的距离以及棱锥的体积计算,考查计算能力.本题的难点在于点G到平面BFD1E的距离对应的垂线段不好找.

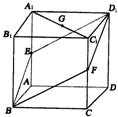 如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E、F分别是棱AA1和CC1的中点,G是A1C1的中点,求:
如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E、F分别是棱AA1和CC1的中点,G是A1C1的中点,求:

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
 (2012•汕头二模)如图,已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,
(2012•汕头二模)如图,已知ABCD-A1B1C1D1是底面边长为1的正四棱柱, 如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.
如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE. (2005•普陀区一模)如图,已知ABCD和A1B1C1D1都是正方形,且AB∥A1B1,AA1=BB1=CC1=DD1,若将图中已作出的线段的两个端点分别作为向量的始点和终点所形成的不相等的向量的全体构成集合M,则从集合M中任取两个向量恰为平行向量的概率是
(2005•普陀区一模)如图,已知ABCD和A1B1C1D1都是正方形,且AB∥A1B1,AA1=BB1=CC1=DD1,若将图中已作出的线段的两个端点分别作为向量的始点和终点所形成的不相等的向量的全体构成集合M,则从集合M中任取两个向量恰为平行向量的概率是