
【题目】理科竞赛小组有9名女生、12名男生,从中随机抽取一个容量为7的样本进行分析.
(Ⅰ)如果按照性别比例分层抽样,可以得到多少个不同的样本?(写出算式即可)
(Ⅱ)如果随机抽取的7名同学的物理、化学成绩(单位:分)对应如表:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
物理成绩 | 65 | 70 | 75 | 81 | 85 | 87 | 93 |
化学成绩 | 72 | 68 | 80 | 85 | 90 | 86 | 91 |
规定85分以上(包括85份)为优秀,从这7名同学中再抽取3名同学,记这3名同学中物理和化学成绩均为优秀的人数为X,求随机变量X的分布列和数学期望.
【答案】解:(Ⅰ)如果按照性别比例分层抽样,则从9名女生、12名男生, 从中随机抽取一个容量为7的样本,抽取的女生为3人,男生为4人.可以得到 ![]() 个不同的样本.
个不同的样本.
(II)这7名同学中物理和化学成绩均为优秀的人数为3人,
抽取的3名同学中物理和化学成绩均为优秀的人数X可能取值为0,1,2,3,
则P(X=k)= ![]() ,可得P(X=0)=
,可得P(X=0)= ![]() ,P(X=1)=
,P(X=1)= ![]() ,P(X=2)=
,P(X=2)= ![]() ,P(X=3)=
,P(X=3)= ![]() .
.
其X分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
数学期望E(X)=0+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =
= ![]() .
.
【解析】(Ⅰ)如果按照性别比例分层抽样,则从9名女生、12名男生,从中随机抽取一个容量为7的样本,抽取的女生为3人,男生为4人.利用组合数的意义即可得出.(II)这7名同学中物理和化学成绩均为优秀的人数为3人,抽取的3名同学中物理和化学成绩均为优秀的人数X可能取值为0,1,2,3,可得P(X=k)= ![]() ,即可得出分布列与数学期望计算公式.
,即可得出分布列与数学期望计算公式.


科目:高中数学 来源: 题型:
【题目】如图,点F1、F2是椭圆C1的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2 , 椭圆C1与双曲线C2的离心率分别为e1、e2 , 则( ) 
A.e22= ![]()
B.e22= ![]()
C.e22= ![]()
D.e22= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 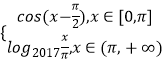 ,若有三个不同的实数a,b,c,使得f(a)=f(b)=f(c),则a+b+c的取值范围为( )
,若有三个不同的实数a,b,c,使得f(a)=f(b)=f(c),则a+b+c的取值范围为( )
A.(2π,2017π)
B.(2π,2018π)
C.( ![]() ,
, ![]() )
)
D.(π,2017π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
(Ⅰ)求证:CE∥平面PAD;
(Ⅱ)求PD与平面PCE所成角的正弦值;
(Ⅲ)在棱AB上是否存在一点F,使得平面DEF⊥平面PCE?如果存在,求 ![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a>b>0)的离心率
(a>b>0)的离心率 ![]() ,且点
,且点 ![]() 在椭圆E上.
在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)直线l与椭圆E交于A、B两点,且线段AB的垂直平分线经过点 ![]() .求△AOB(O为坐标原点)面积的最大值.
.求△AOB(O为坐标原点)面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知关于![]() 的不等式
的不等式![]() ,其中
,其中![]() .
.
(1)当![]() 变化时,试求不等式的解集
变化时,试求不等式的解集![]() ;
;
(2)对于不等式的解集![]() ,若满足
,若满足![]() (其中
(其中![]() 为整数集). 试探究集合
为整数集). 试探究集合![]() 能否为有限集?若 能,求出使得集合
能否为有限集?若 能,求出使得集合![]() 中元素个数最少的
中元素个数最少的![]() 的所有取值,并用列举法表示集合
的所有取值,并用列举法表示集合![]() ;若不能,请说明理由.
;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义[x]表示不超过x的最大整数,例如[2.11]=2,[﹣1.39]=﹣2,执行如下图所示的程序框图,则输出m的值为 ( )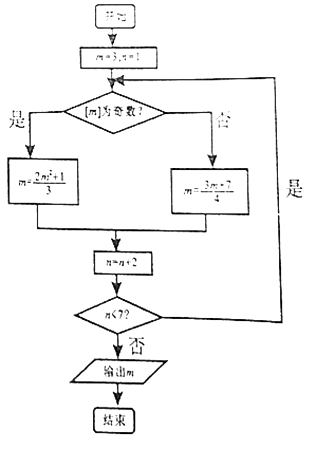
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,数列{bn}是等比数列,Sn是数列{an}的前n项和,a1=b1=1,S2=![]() .
.
(1)若b2是a1,a3的等差中项,求数列{an}与{bn}的通项公式;
(2)若an∈N+,数列{![]() }是公比为9的等比数列,求证:
}是公比为9的等比数列,求证:![]() +
+![]() +
+![]() +…+
+…+![]() <
<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为F,A(x1,y1),B(x2,y2)是过F的直线与抛物线的两个交点,求证:
(1)y1y2=-p2,![]() ;(2)
;(2)![]() 为定值;
为定值;
(3)以AB为直径的圆与抛物线的准线相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com